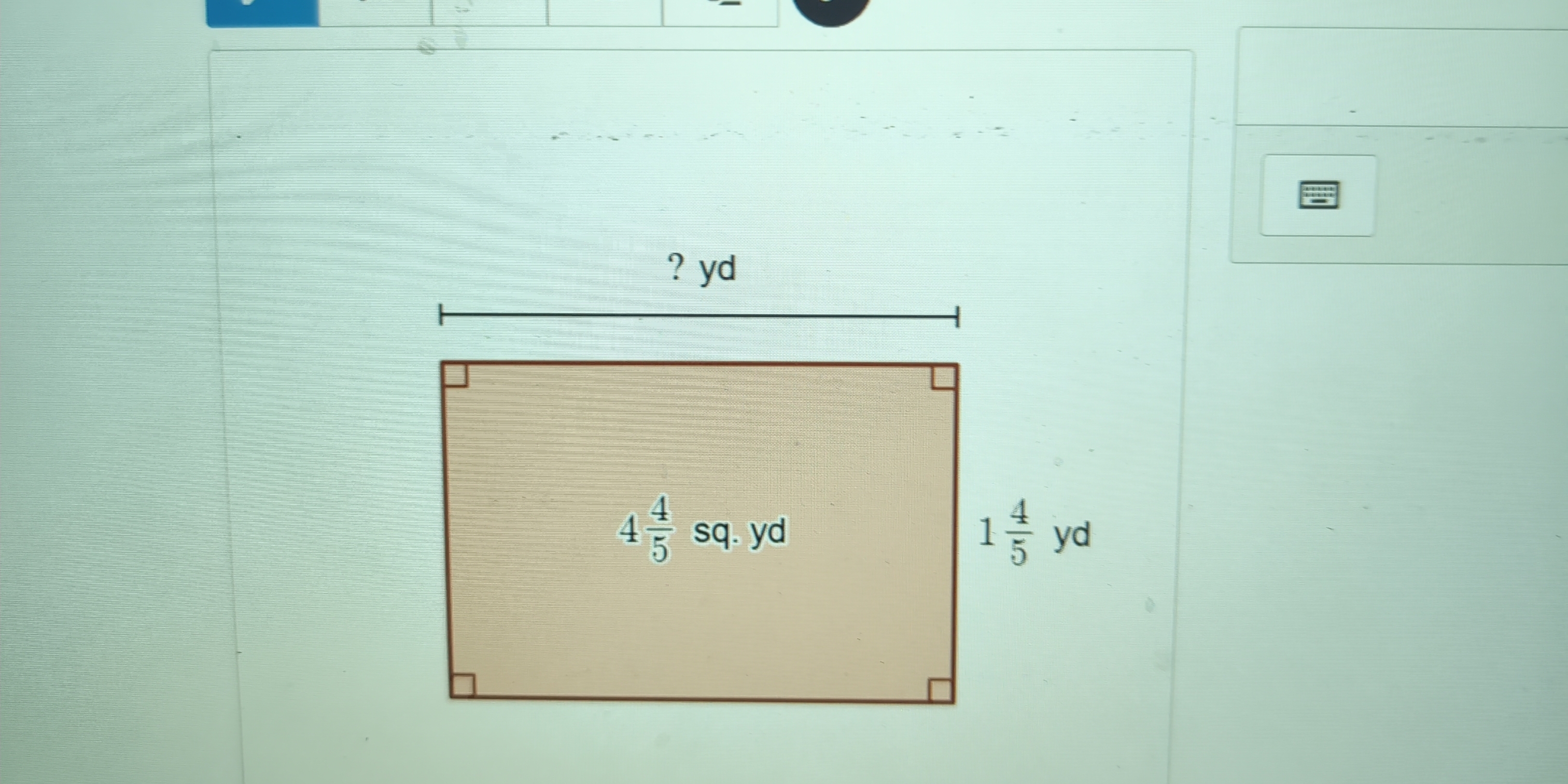
What is the width of a rectangle with an area of 4 4/5 square yards and a length of 1 4/5 yards?

Steps to Solve

1. Convert Mixed Numbers to Improper Fractions

First, we need to convert the mixed numbers into improper fractions for easier calculations.

The area ( 4 \frac{4}{5} = \frac{24}{5} ) (since ( 4 \times 5 + 4 = 24 )).

The length ( 1 \frac{4}{5} = \frac{9}{5} ) (since ( 1 \times 5 + 4 = 9 )).

2. Using Area Formula to Find Width

The area ( A ) of a rectangle is given by the formula:

$$ A = \text{length} \times \text{width} $$

We can rearrange this to find the width (( w )):

$$ w = \frac{A}{\text{length}} $$

Substituting the values we have:

$$ w = \frac{\frac{24}{5}}{\frac{9}{5}} $$

3. Simplifying the Width Calculation

To simplify the fraction, we multiply by the reciprocal of the denominator:

$$ w = \frac{24}{5} \times \frac{5}{9} $$

4. Final Calculation for Width

The ( 5 ) in the numerator and denominator cancel:

$$ w = \frac{24}{9} $$

Now simplify this fraction:

$$ w = \frac{8}{3} $$

5. Convert Back to Mixed Number

To convert ( \frac{8}{3} ) back to a mixed number:

$$ 8 \div 3 = 2 \text{ R } 2 $$

So, ( \frac{8}{3} = 2 \frac{2}{3} ).