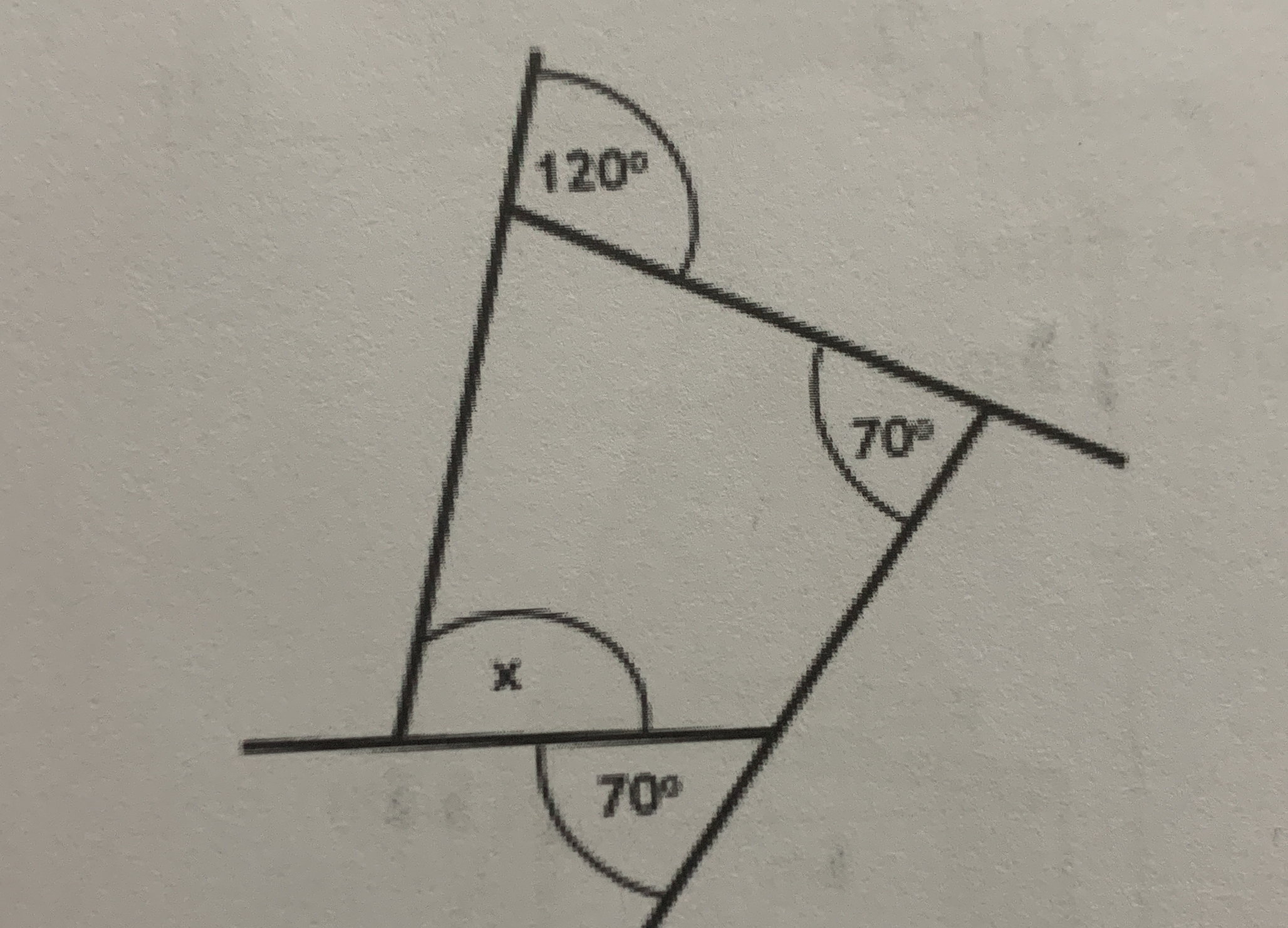
What is the value of x in the given triangle diagram?
Understand the Problem
The question is asking to determine the value of the angle 'x' in a geometric figure involving angles of 120° and 70°. The solution involves applying the properties of angles, particularly the fact that the sum of the angles at a point equals 180°.
Answer
$x = 60^\circ$
Answer for screen readers
The value of angle $x$ is $60^\circ$.
Steps to Solve
-
Identify the angles related to 'x'
The geometry shows that angle 'x' is supplementary to the angle of $120^\circ$ on the same line. Therefore, we can use the relationship that the sum of angles on a straight line is $180^\circ$. -
Set up the equation
To express the relationship, we set up the equation:
$$ x + 120^\circ = 180^\circ $$ -
Solve for 'x'
To find 'x', subtract $120^\circ$ from both sides of the equation: $$ x = 180^\circ - 120^\circ $$ -
Calculate 'x'
Now perform the subtraction: $$ x = 60^\circ $$
The value of angle $x$ is $60^\circ$.
More Information
In this problem, the key property used is that angles on a straight line sum to $180^\circ$. This concept is fundamental in geometry and helps in solving various angle-related problems.
Tips
- A common mistake is forgetting that the angles on a straight line must sum to $180^\circ$. Always double-check the setup of the equation.
AI-generated content may contain errors. Please verify critical information