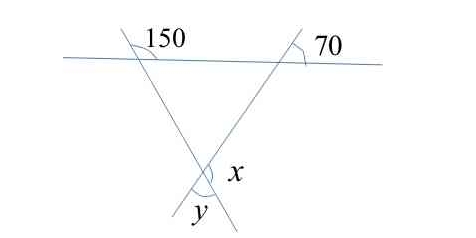
What is the value of x and y in the given figure?
Understand the Problem
The question involves finding the values of the angles labeled x and y in relation to the given angles of 150 and 70 degrees. We can use the properties of supplementary and vertical angles to solve for x and y.
Answer
The values are \( x = 30^\circ \) and \( y = 110^\circ \).
Answer for screen readers
The values are ( x = 30^\circ ) and ( y = 110^\circ ).
Steps to Solve
-
Identify Relationships Between Angles
In the diagram, angle 150 degrees and angle x are supplementary angles. This means they add up to 180 degrees.
The equation is:
$$ 150 + x = 180 $$
-
Solve for x
Subtract 150 from both sides to isolate x:
$$ x = 180 - 150 $$
$$ x = 30 $$
-
Identify Relationship for y
Angle 70 degrees and angle y are also supplementary angles, so they also add up to 180 degrees.
The equation is:
$$ 70 + y = 180 $$
-
Solve for y
Subtract 70 from both sides to isolate y:
$$ y = 180 - 70 $$
$$ y = 110 $$
The values are ( x = 30^\circ ) and ( y = 110^\circ ).
More Information
The angles in the figure are derived from the properties of supplementary angles. Supplementary angles are those that sum up to 180 degrees, which is essential in solving angle-related problems in geometry.
Tips
- Confusing supplementary and complementary angles. Remember, supplementary angles add up to 180 degrees, while complementary angles add up to 90 degrees.
- Forgetting to subtract properly when isolating the variable. Always double-check your arithmetic.
AI-generated content may contain errors. Please verify critical information