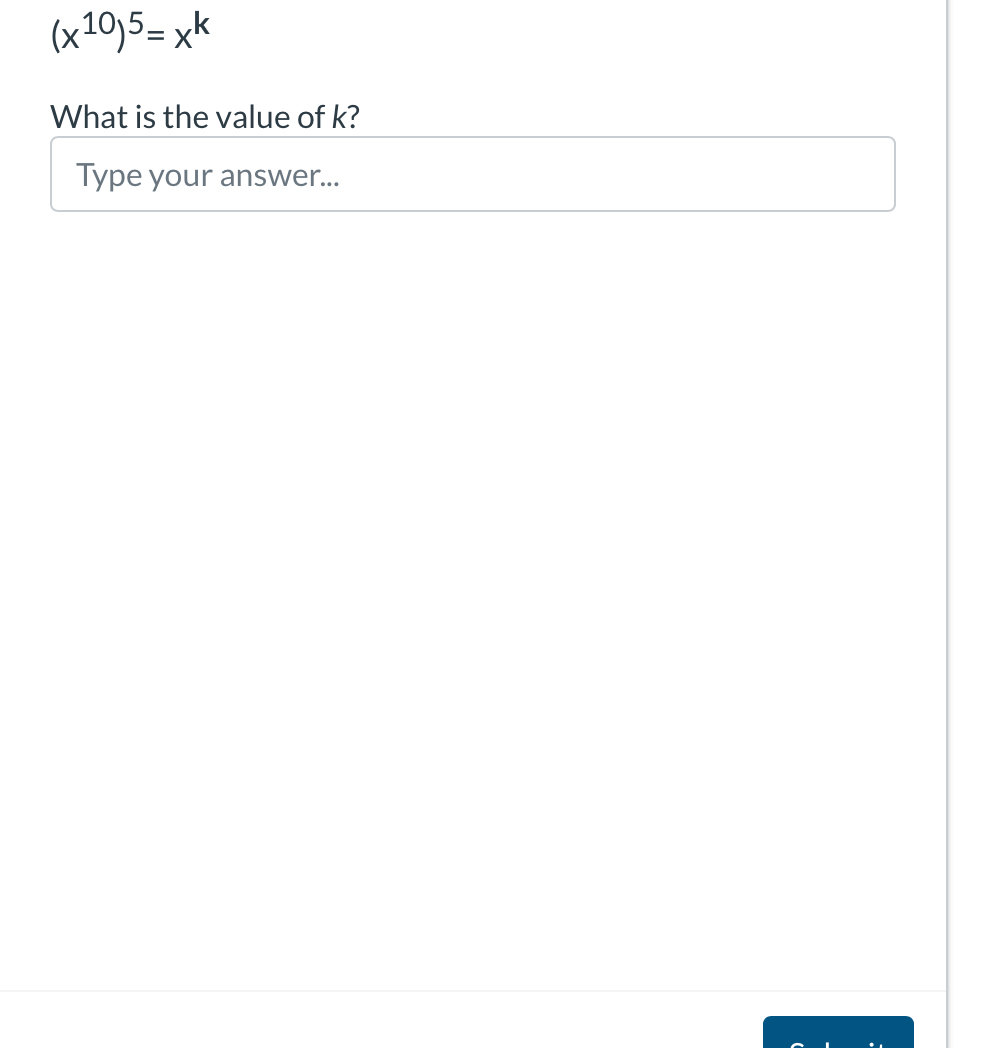
What is the value of k in the equation (x^10)^5 = x^k?
Understand the Problem
The question is asking for the value of k in the equation (x^{10})^5 = x^k. To solve it, we will use the properties of exponents to simplify the left side of the equation and then equate the exponents.
Answer
The value of $k$ is $50$.
Answer for screen readers
The value of $k$ is $50$.
Steps to Solve
- Apply the Power of a Power Rule
To simplify the left side of the equation $(x^{10})^5$, use the power of a power property: $(a^m)^n = a^{mn}$. Therefore, we can rewrite it as: $$ (x^{10})^5 = x^{10 \cdot 5} $$
- Calculate the Exponents
Now, calculate the exponent: $$ 10 \cdot 5 = 50 $$
So, we have: $$ (x^{10})^5 = x^{50} $$
- Set the Exponents Equal
We can now equate the exponents from both sides of the equation: $$ 50 = k $$
The value of $k$ is $50$.
More Information
In exponent rules, when raising a power to another power, you multiply the exponents. Here, we multiplied $10$ by $5$ to find the exponent on the left side.
Tips
- Forgetting to multiply the exponents correctly when using the power of a power rule.
- Confusing $x^{mn}$ with $x^{m+n}$, which is a common error.
AI-generated content may contain errors. Please verify critical information