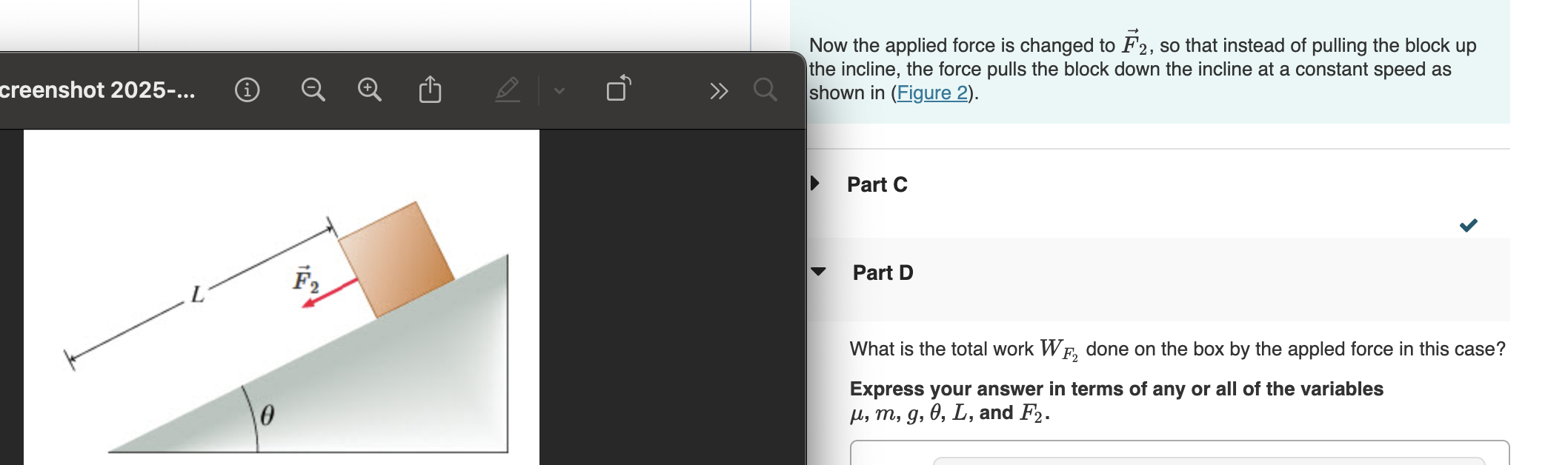
What is the total work W₂ done on the box by the applied force in this case? Express your answer in terms of any or all of the variables μ, m, g, θ, L, and F₂.

Steps to Solve

1. Identify the Forces Acting on the Box

The box on the incline experiences several forces:

• The weight of the box, $W = mg$, acting downward.
• The normal force $N$ acting perpendicular to the surface.
• The applied force $F_2$ acting down the incline.
• The frictional force $f = \mu N$ opposing the motion.

2. Resolve the Forces

The weight can be resolved into two components:

• Parallel to the incline: $W_{\parallel} = mg \sin \theta$
• Perpendicular to the incline: $W_{\perpendicular} = mg \cos \theta$

3. Apply Newton's Second Law

Since the box moves at a constant speed, the net force along the incline is zero. Thus, we can write: $$ F_2 - f - W_{\parallel} = 0 $$

Substituting for the frictional force ($f$): $$ F_2 - \mu N - mg \sin \theta = 0 $$

4. Express the Normal Force

The normal force $N$ is equal to the perpendicular component of the weight: $$ N = mg \cos \theta $$

5. Substitute Normal Force Back into the Equation

Substituting $N$ into the previous equation gives: $$ F_2 - \mu (mg \cos \theta) - mg \sin \theta = 0 $$

Rearranging gives: $$ F_2 = \mu (mg \cos \theta) + mg \sin \theta $$

6. Calculate the Work Done by the Applied Force

The work done by the force $F_2$ over a distance $L$ is given by the formula: $$ W_{F_2} = F_2 \cdot L $$

Substitute $F_2$: $$ W_{F_2} = \left( \mu (mg \cos \theta) + mg \sin \theta \right) L $$