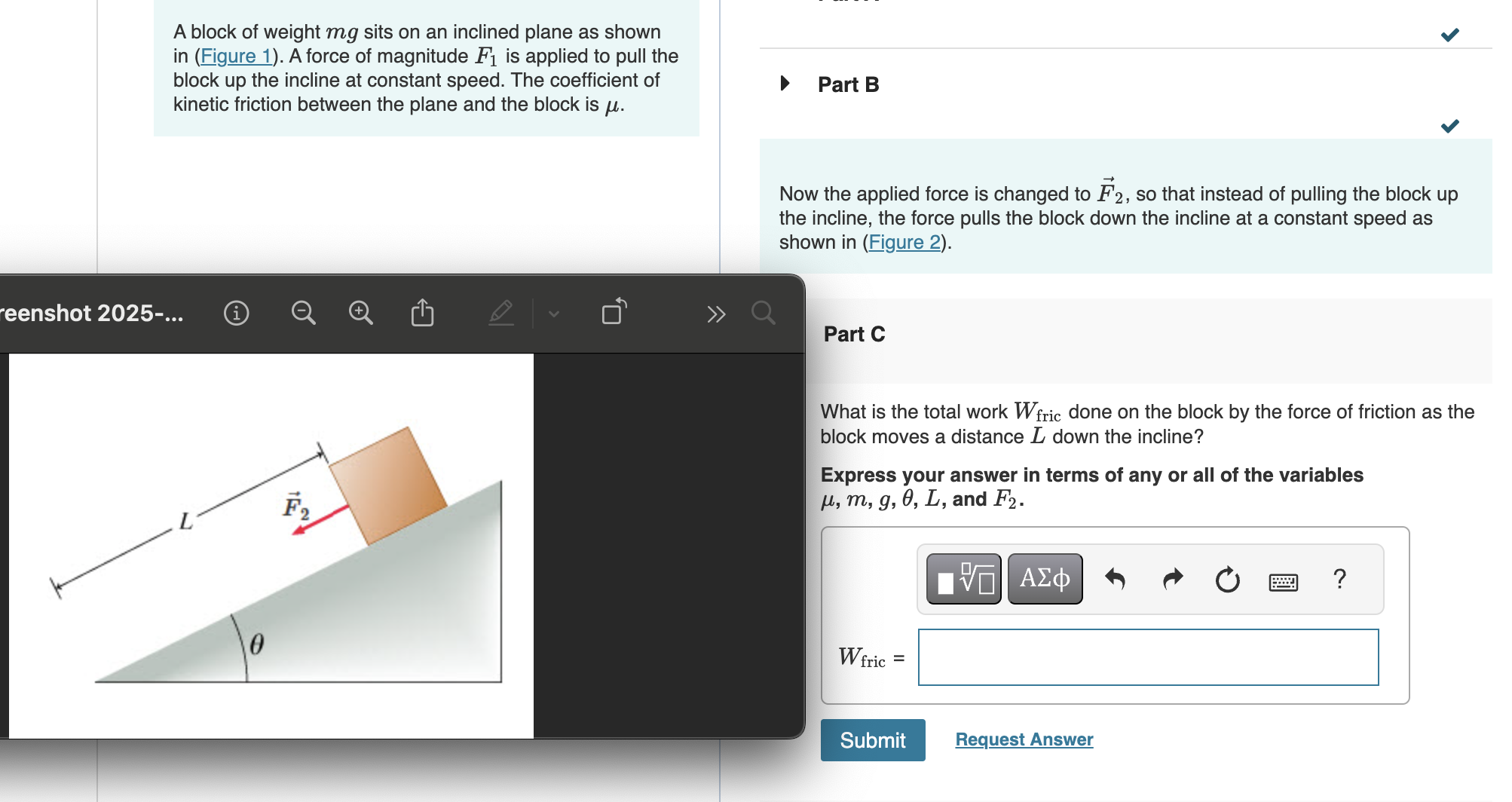
What is the total work W_fric done on the block by the force of friction as the block moves a distance L down the incline? Express your answer in terms of any or all of the variabl... What is the total work W_fric done on the block by the force of friction as the block moves a distance L down the incline? Express your answer in terms of any or all of the variables mu, m, g, L, and F2.
Understand the Problem
The question is asking for the total work done on a block by the force of friction as it moves down an incline. To solve this, we need to calculate the work using the coefficient of friction, gravitational force, and the distance the block travels down the incline.
Answer
The work done by friction is given by the equation: $$ W_{fric} = -\mu (mg \cos(\theta)) L $$
Answer for screen readers
The total work done by the force of friction is: $$ W_{fric} = -\mu (mg \cos(\theta)) L $$
Steps to Solve
- Identify the Forces Acting on the Block
The forces acting on the block as it moves down the incline include the force of gravity, the normal force, and friction. We can start by determining these forces:
- The gravitational force acting on the block is $F_g = mg$.
- The normal force $F_n$ can be calculated using the angle $\theta$: $$ F_n = mg \cos(\theta) $$
- Calculate the Force of Friction
The force of kinetic friction can be calculated using the coefficient of kinetic friction $\mu$ and the normal force $F_n$. The formula for the force of friction $F_{fric}$ is: $$ F_{fric} = \mu F_n = \mu (mg \cos(\theta)) $$
- Determine the Work Done by Friction
The work done by the force of friction as the block moves a distance $L$ down the incline (in the direction opposite to the movement) can be calculated using the formula: $$ W_{fric} = -F_{fric} \cdot d $$ Where $d = L$. Therefore, substituting for $F_{fric}$ we get: $$ W_{fric} = -\mu (mg \cos(\theta)) L $$
- Finalizing the Expression for Work Done by Friction
So, the total work done by the force of friction can be expressed as: $$ W_{fric} = -\mu (mg \cos(\theta)) L $$
The total work done by the force of friction is: $$ W_{fric} = -\mu (mg \cos(\theta)) L $$
More Information
The negative sign indicates that the work done by friction opposes the direction of motion. This is a typical scenario in physics, where friction always acts against the movement of an object, resulting in energy loss.
Tips
- Forgetting to include the negative sign when calculating work done by friction can result in an incorrect positive work value, leading to misunderstandings about energy transfer.
- Miscalculating the normal force or the friction force can lead to incorrect values for work.
AI-generated content may contain errors. Please verify critical information