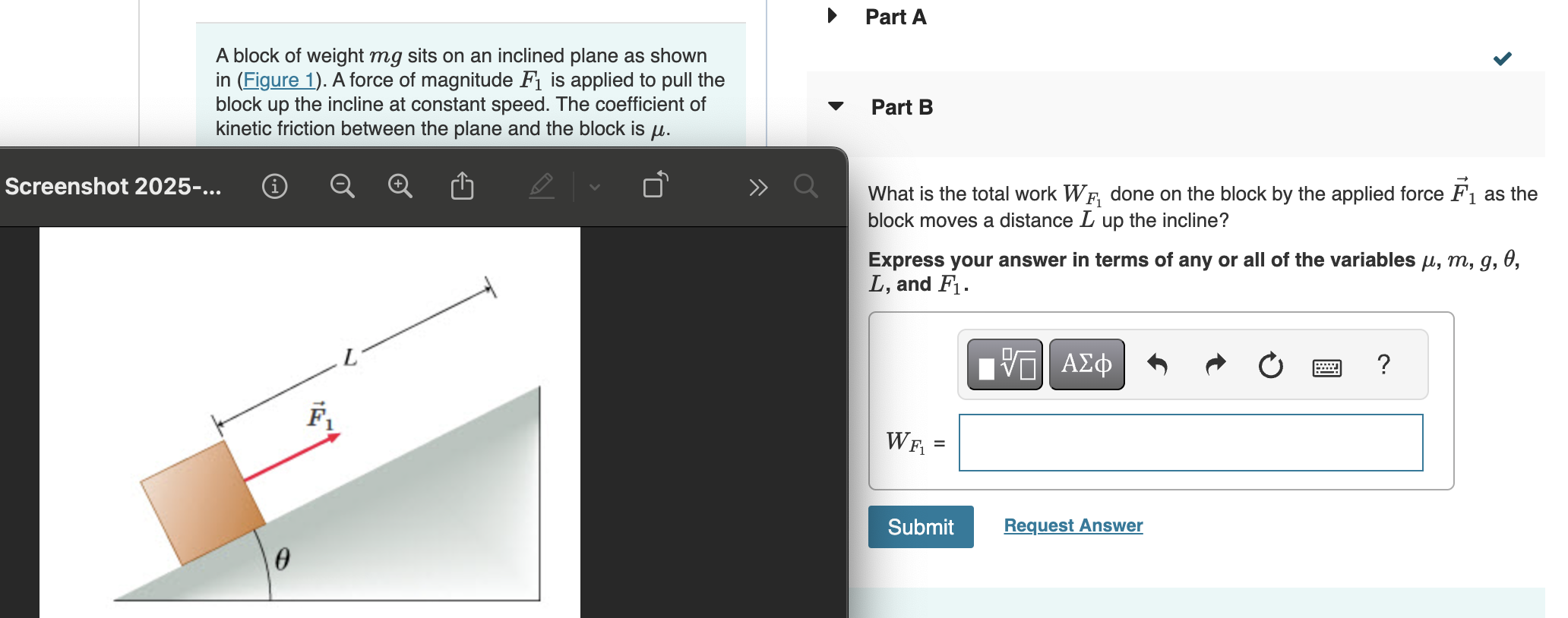
What is the total work done on the block by the applied force as the block moves a distance up the incline? Express your answer in terms of any or all of the variables μ, m, g, L,... What is the total work done on the block by the applied force as the block moves a distance up the incline? Express your answer in terms of any or all of the variables μ, m, g, L, and F1. Read more

Steps to Solve

1. Identify Forces Acting on the Block The forces acting on the block include:

• The gravitational force ($F_g = mg$) acting downwards.
• The normal force ($F_N$) acting perpendicular to the incline.
• The frictional force ($F_f = \mu F_N$) acting down the incline.
• The applied force ($F_1$) acting up the incline.

2. Calculate the Normal Force The normal force can be found using the weight of the block and the angle of the incline: $$ F_N = mg \cos(\theta) $$

3. Calculate the Frictional Force Now, substitute the normal force into the frictional force equation: $$ F_f = \mu F_N = \mu (mg \cos(\theta)) $$

4. Apply Newton's Second Law Since the block is moving up the incline at constant speed, the net force along the incline is zero: $$ F_1 - F_f - F_g \sin(\theta) = 0 $$ Substituting the expressions for the forces: $$ F_1 - \mu (mg \cos(\theta)) - mg \sin(\theta) = 0 $$

5. Solve for the Applied Force $F_1$ Rearranging the equation gives: $$ F_1 = mg \sin(\theta) + \mu (mg \cos(\theta)) $$

6. Calculate the Work Done by the Applied Force Work done by the applied force as the block moves a distance $L$ is: $$ W_{F_1} = F_1 \cdot L $$ Now substitute $F_1$ from the previous step into this equation: $$ W_{F_1} = \left( mg \sin(\theta) + \mu (mg \cos(\theta)) \right) L $$