What is the total resultant force on the object and at what angle is it applied?
Understand the Problem
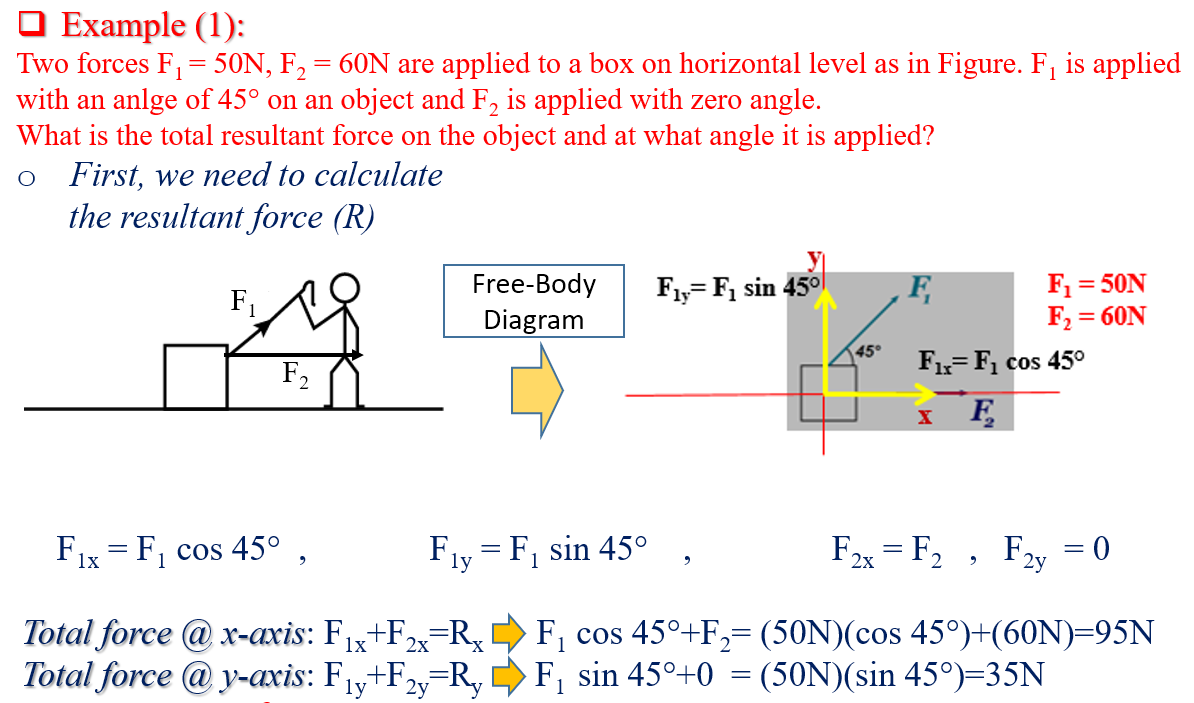
The question involves calculating the resultant force (R) acting on an object when two forces, F1 and F2, are applied at specified angles. It asks for both the magnitude of the resultant force and the angle at which it acts, based on the vector components of the forces.
Answer
The resultant force is $R \approx 95N$ at an angle $\theta \approx 20.5^\circ$ above the horizontal.
Answer for screen readers
The magnitude of the resultant force is approximately $R = 95N$ and the angle is $\theta \approx 20.5^\circ$.
Steps to Solve
- Calculate the x-component of F1
The x-component of the force $F_1$ can be calculated using the cosine function: $$ F_{1x} = F_1 \cos 45^\circ = 50 \cos 45^\circ $$
- Calculate the y-component of F1
The y-component of the force $F_1$ can be calculated using the sine function: $$ F_{1y} = F_1 \sin 45^\circ = 50 \sin 45^\circ $$
- Add the components of F2
Since $F_2 = 60N$ is acting horizontally (along the x-axis) and has no y-component: $$ F_{2x} = F_2 = 60N $$ $$ F_{2y} = 0N $$
- Calculate total force in x-direction
Combine the x-components to find the total force in the x-direction ($R_x$): $$ R_x = F_{1x} + F_{2x} = (50 \cos 45^\circ) + 60 $$
- Calculate total force in y-direction
Combine the y-components to find the total force in the y-direction ($R_y$): $$ R_y = F_{1y} + F_{2y} = (50 \sin 45^\circ) + 0 $$
- Calculate the magnitude of the resultant force (R)
Using the Pythagorean theorem to find the magnitude of the resultant force: $$ R = \sqrt{R_x^2 + R_y^2} $$
- Calculate the angle of the resultant force (θ)
Determine the angle at which the resultant force acts using the inverse tangent function: $$ \theta = \tan^{-1}\left(\frac{R_y}{R_x}\right) $$
The magnitude of the resultant force is approximately $R = 95N$ and the angle is $\theta \approx 20.5^\circ$.
More Information
The forces acting on the object combine both horizontally and vertically, demonstrating how vector components can be added to yield a resultant force. The angle calculated helps understand the direction of this force relative to the horizontal.
Tips
- Confusing the sine and cosine functions when calculating the components.
- Forgetting to include one of the forces in the total calculations for either the x or y direction.
- Misapplying the Pythagorean theorem for calculating the resultant magnitude.
AI-generated content may contain errors. Please verify critical information