What is the tangent ratio and how do you relate it to the angle of inclination of a line segment?
Understand the Problem
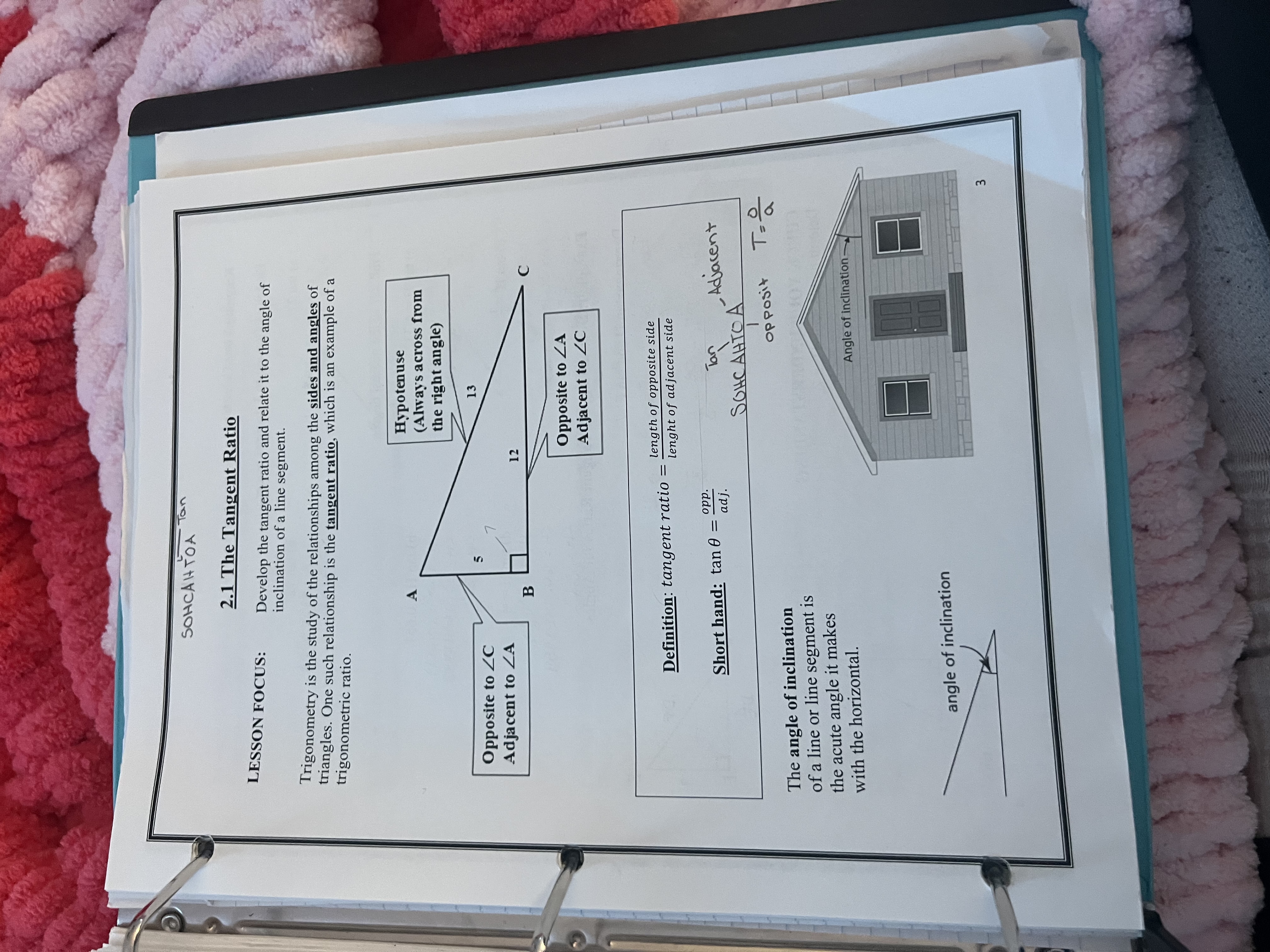
The question relates to the concept of the tangent ratio in trigonometry, which involves the relationship between the sides and angles of a right triangle. It specifically focuses on how to calculate the tangent of an angle using the lengths of the opposite and adjacent sides.
Answer
The angle \( A \) is approximately $22.6^\circ$.
Answer for screen readers
The angle ( A ) is approximately ( 22.6^\circ ).
Steps to Solve
- Identify the sides of the triangle
In the given triangle ABC, the lengths of the sides are provided as follows:
- Opposite side to angle ( A ) (side ( BC )) = ( 5 )
- Adjacent side to angle ( A ) (side ( AB )) = ( 12 )
- Use the tangent ratio
The tangent ratio for angle ( A ) can be calculated using the formula: $$ \tan A = \frac{\text{Opposite}}{\text{Adjacent}} $$
Substituting the known values: $$ \tan A = \frac{5}{12} $$
- Calculate the tangent value
To find the decimal value of ( \tan A ): $$ \tan A \approx 0.4167 $$
This is the approximate value of the tangent of angle ( A ).
- Determine the angle ( A )
To find the angle ( A ), we use the inverse tangent function ( \tan^{-1} ): $$ A = \tan^{-1}\left(\frac{5}{12}\right) $$
Using a calculator: $$ A \approx 22.6^\circ $$
The angle ( A ) is approximately ( 22.6^\circ ).
More Information
The tangent ratio provides a mathematical way to relate the angles and side lengths of a right triangle. It is useful in various applications, including architecture, physics, and engineering, for calculating angles of inclination and slopes.
Tips
- Misidentifying sides: Confusing opposite and adjacent sides can lead to incorrect calculations of the tangent.
- Forgetting the inverse function: When trying to find the angle from the tangent value, forgetting to use the inverse tangent can result in confusion.
- Using incorrect units: Always ensure to work with consistent units when calculating lengths in geometric problems.
AI-generated content may contain errors. Please verify critical information