What is the sum of roots of the equation (x^2 - 3x)^2 - (3x^2 - 9x) = 4?
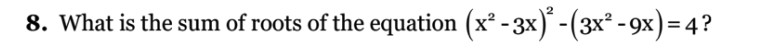
Understand the Problem
The question is asking for the sum of the roots of a given equation involving polynomial expressions. To solve it, we will first need to simplify the equation and then apply the properties of polynomial roots.
Answer
The sum of the roots is \( 6 \).
Answer for screen readers
The sum of the roots of the equation is ( 6 ).
Steps to Solve
-
Rewrite the equation Rewrite the equation to isolate everything on one side. The original equation is $$(x^2 - 3x)^2 - (3x^2 - 9x) = 4.$$ Rearranging gives $$(x^2 - 3x)^2 - (3x^2 - 9x) - 4 = 0.$$
-
Simplify the equation Next, substitute ( y = x^2 - 3x ) into the equation. This changes the left side to: $$y^2 - (3(x^2 - 3x)) - 4 = 0 \rightarrow y^2 - (3y) - 4 = 0.$$
-
Apply the quadratic formula Now, apply the quadratic formula to solve for ( y ): $$y = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$ where ( a = 1, b = -3, c = -4 ). So, $$y = \frac{3 \pm \sqrt{(-3)^2 - 4(1)(-4)}}{2(1)}.$$
-
Calculate the discriminant Calculate the discriminant: $$(-3)^2 - 4(1)(-4) = 9 + 16 = 25.$$ So, $$y = \frac{3 \pm 5}{2}.$$
-
Find the values of ( y ) Now, solve for ( y ):
- First root: ( y = \frac{3 + 5}{2} = 4 )
- Second root: ( y = \frac{3 - 5}{2} = -1 )
- Revert to ( x ) and find the roots Now revert to the original variable ( x ):
- From ( y = x^2 - 3x = 4 ): $$x^2 - 3x - 4 = 0$$ Using the quadratic formula, we get: $$x = \frac{3 \pm \sqrt{(3)^2 - 4(1)(-4)}}{2(1)}$$ Calculate the roots and sum.
- From ( y = x^2 - 3x = -1 ): $$x^2 - 3x + 1 = 0$$ Using the quadratic formula, we get the roots and sum.
- Sum the Roots The sum of roots for a quadratic ( ax^2 + bx + c ) is given by ( -\frac{b}{a} ). For ( y = 4 ): The sum is ( 3 ).
For ( y = -1 ): The sum is ( 3 ) again.
So, total sum = ( 3 + 3 = 6 ).
The sum of the roots of the equation is ( 6 ).
More Information
The sum of the roots can be calculated using Vieta's formulas, which state that for a quadratic equation ( ax^2 + bx + c = 0 ), the sum of the roots is given by ( -\frac{b}{a} ). In this problem, both simplified equations yielded the same sum for their roots.
Tips
- Not isolating the terms correctly when rearranging the equation, which could lead to incorrect roots.
- Forgetting to calculate both sets of roots from the factored form of ( y ) might lead to an incomplete sum.
AI-generated content may contain errors. Please verify critical information