What is the solution for the inequality -3x - 19 < -18?
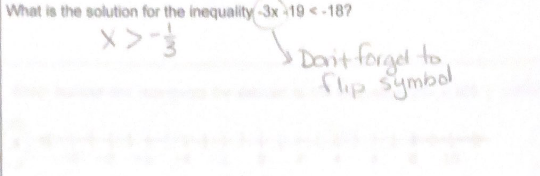
Understand the Problem
The question is asking for the solution to the inequality involving the expression -3x - 19 < -18. It suggests that X > -1/3 and notes to flip the symbol, indicating a need to solve the inequality step-by-step.
Answer
The solution is $x > -\frac{1}{3}$.
Answer for screen readers
The solution for the inequality is:
$$ x > -\frac{1}{3} $$
Steps to Solve
- Isolate the term with $x$
Start by adding $19$ to both sides of the inequality to move the constant term. This gives:
$$ -3x - 19 + 19 < -18 + 19 $$
Resulting in:
$$ -3x < 1 $$
- Divide by the coefficient of $x$
Next, to isolate $x$, divide both sides of the inequality by $-3$. Remember that when dividing by a negative number, we must flip the inequality symbol:
$$ \frac{-3x}{-3} > \frac{1}{-3} $$
Which leads to:
$$ x > -\frac{1}{3} $$
The solution for the inequality is:
$$ x > -\frac{1}{3} $$
More Information
The inequality $-3x - 19 < -18$ simplifies to $x > -\frac{1}{3}$. This means any value of $x$ greater than $-\frac{1}{3}$ satisfies the original inequality.
Tips
- Not flipping the inequality symbol: When dividing or multiplying both sides of an inequality by a negative number, remember to flip the symbol.
- Incorrect arithmetic operations: Double-check each step when adding or subtracting constants.
AI-generated content may contain errors. Please verify critical information