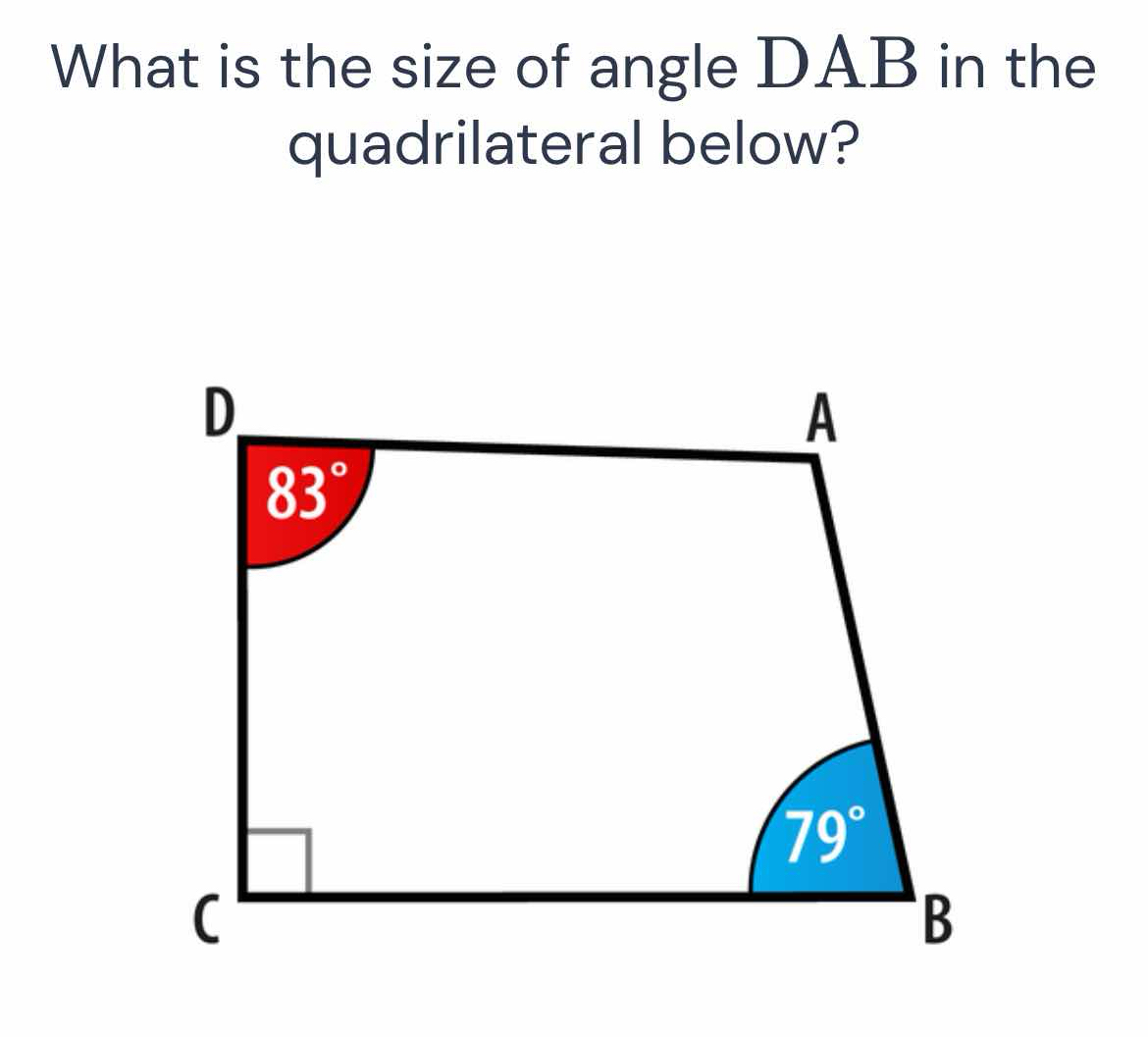
What is the size of angle DAB in the quadrilateral below?
Understand the Problem
The question is asking to find the size of angle DAB in the given quadrilateral, based on the angles provided at points D (83°) and B (79°). The total sum of angles in a quadrilateral is 360°, so we will use this information to calculate angle DAB.
Answer
The angle DAB is $108^\circ$.
Answer for screen readers
The size of angle DAB is $108^\circ$.
Steps to Solve
- Identify Given Angles
The problem provides the following angles:
- Angle D (at point D) = $83^\circ$
- Angle B (at point B) = $79^\circ$
- Angle C (at point C) is a right angle, so Angle C = $90^\circ$.
- Use the Sum of Angles in a Quadrilateral
The sum of the angles in a quadrilateral is given by the equation:
$$ \text{Angle D} + \text{Angle A} + \text{Angle B} + \text{Angle C} = 360^\circ $$
Substituting the known values:
$$ 83^\circ + \text{Angle A} + 79^\circ + 90^\circ = 360^\circ $$
- Combine Known Angles
Combine the known angles:
$$ 83^\circ + 79^\circ + 90^\circ = 252^\circ $$
Now substitute this sum back into the equation:
$$ 252^\circ + \text{Angle A} = 360^\circ $$
- Solve for Angle A
To find Angle A (which is angle DAB), subtract the sum of the known angles from 360°:
$$ \text{Angle A} = 360^\circ - 252^\circ $$
Calculating this gives:
$$ \text{Angle A} = 108^\circ $$
The size of angle DAB is $108^\circ$.
More Information
In any quadrilateral, knowing just three angles allows you to find the fourth angle using the property that the sum of all interior angles always equals $360^\circ$. This method can be applied in various geometrical problems involving polygons.
Tips
- A common mistake is forgetting that angle C is a right angle (which equals $90^\circ$) and not including it in the sum.
- Another mistake is miscalculating the subtraction from $360^\circ$. To avoid this, double-check the addition of the known angles before subtracting.
AI-generated content may contain errors. Please verify critical information