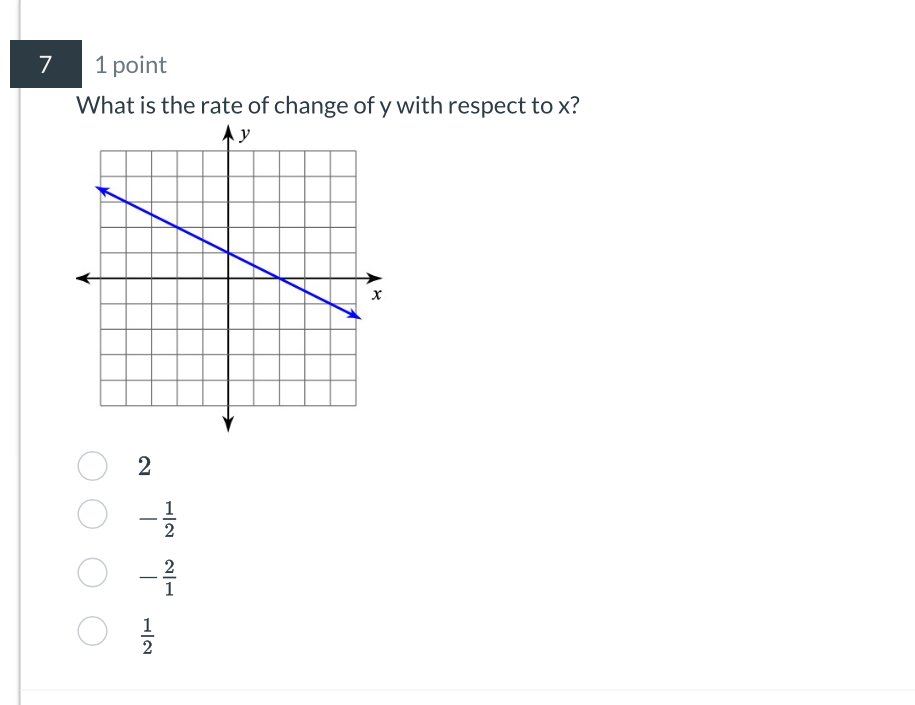
What is the rate of change of y with respect to x?
Understand the Problem
The question is asking for the rate of change of y with respect to x, which refers to the slope of the line depicted in the graph. We will determine the slope using points on the line and apply the slope formula.
Answer
The rate of change of \( y \) with respect to \( x \) is \( -\frac{1}{2} \).
Answer for screen readers
The rate of change of ( y ) with respect to ( x ) is ( -\frac{1}{2} ).
Steps to Solve
-
Identify Two Points on the Line Choose two clear points from the line in the graph. For example, let's say the points are ( (2, 1) ) and ( (0, 2) ).
-
Calculate the Change in y (Rise) Calculate the difference in the y-coordinates of the two points: $$ \Delta y = y_2 - y_1 = 2 - 1 = 1 $$
-
Calculate the Change in x (Run) Calculate the difference in the x-coordinates of the two points: $$ \Delta x = x_2 - x_1 = 0 - 2 = -2 $$
-
Apply the Slope Formula Use the slope formula (rate of change) given by: $$ m = \frac{\Delta y}{\Delta x} $$
Plugging in the values we calculated: $$ m = \frac{1}{-2} = -\frac{1}{2} $$
The rate of change of ( y ) with respect to ( x ) is ( -\frac{1}{2} ).
More Information
The slope represents the rate at which ( y ) decreases as ( x ) increases. A slope of ( -\frac{1}{2} ) indicates that for every 2 units you move to the right on the x-axis, ( y ) decreases by 1 unit.
Tips
- Mixing up ( \Delta y ) and ( \Delta x ) can lead to an incorrect slope sign.
- Not choosing points accurately or misreading the graph can yield incorrect values.
AI-generated content may contain errors. Please verify critical information