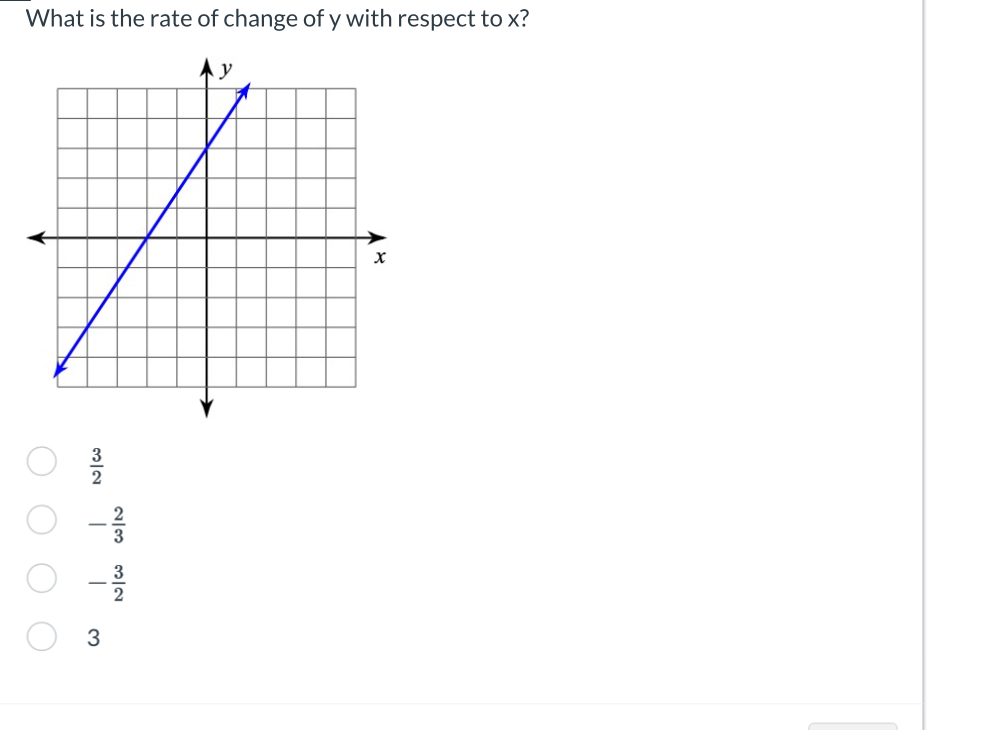
What is the rate of change of y with respect to x?
Understand the Problem
The question is asking for the rate of change of y with respect to x, which refers to the slope of the line represented in the graph. To find this, we will calculate the change in y over the change in x between two points on the line.
Answer
The rate of change of \( y \) with respect to \( x \) is \( \frac{2}{3} \).
Answer for screen readers
The rate of change of ( y ) with respect to ( x ) is ( \frac{2}{3} ).
Steps to Solve
- Identify the points on the line
Locate two points on the line depicted in the graph. For example, we can choose the points (0, 0) and (3, 2).
- Calculate the change in y
Find the change in the y-values between the two points. This is done by subtracting the y-coordinate of the first point from the y-coordinate of the second point:
$$ \Delta y = y_2 - y_1 = 2 - 0 = 2 $$
- Calculate the change in x
Next, find the change in the x-values between the two points by subtracting the x-coordinate of the first point from the x-coordinate of the second point:
$$ \Delta x = x_2 - x_1 = 3 - 0 = 3 $$
- Calculate the slope (rate of change)
The slope of the line, which represents the rate of change of y with respect to x, is calculated using the changes in y and x:
$$ \text{slope} = \frac{\Delta y}{\Delta x} = \frac{2}{3} $$
The rate of change of ( y ) with respect to ( x ) is ( \frac{2}{3} ).
More Information
The rate of change, or slope, indicates how much ( y ) changes for a unit increase in ( x ). In this case, for every 3 units increase in ( x ), ( y ) increases by 2 units.
Tips
- Confusing the order of ( y ) and ( x ) when calculating the slope.
- Choosing points that are too close together and mistakenly calculating the slope based on those.
AI-generated content may contain errors. Please verify critical information