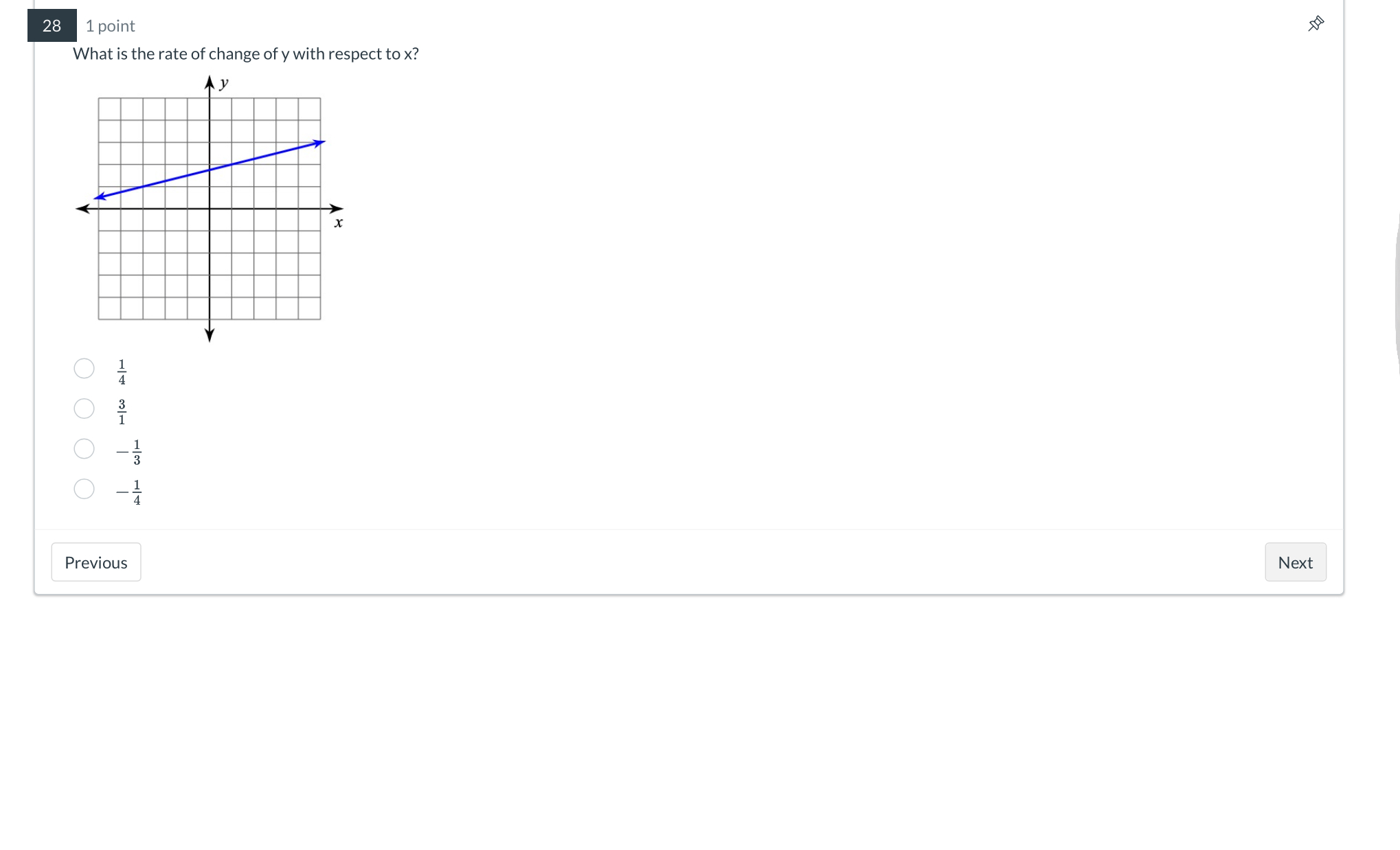
What is the rate of change of y with respect to x?
Understand the Problem
The question is asking for the rate of change of y with respect to x based on a given graph. This involves calculating the slope of the line represented in the graph.
Answer
The rate of change of \( y \) with respect to \( x \) is \( \frac{1}{4} \).
Answer for screen readers
The rate of change of ( y ) with respect to ( x ) is ( \frac{1}{4} ).
Steps to Solve
- Identify Two Points on the Line
Select two clear points on the line. For example, let’s choose point A at (0, 1) and point B at (4, 2).
- Calculate the Change in y (Δy)
Find the difference in the y-coordinates of points A and B:
$$ Δy = y_B - y_A = 2 - 1 = 1 $$
- Calculate the Change in x (Δx)
Now, find the difference in the x-coordinates of points A and B:
$$ Δx = x_B - x_A = 4 - 0 = 4 $$
- Calculate the Slope (Rate of Change)
The slope (rate of change of y with respect to x) can be calculated using the formula:
$$ \text{slope} = \frac{Δy}{Δx} = \frac{1}{4} $$
The rate of change of ( y ) with respect to ( x ) is ( \frac{1}{4} ).
More Information
The slope of a line represents the rate at which ( y ) changes concerning ( x ). A slope of ( \frac{1}{4} ) means that for every 4 units moved along the x-axis, ( y ) increases by 1 unit.
Tips
- Confusing the order of points when calculating ( Δy ) and ( Δx ). Always subtract the coordinates correctly.
- Not simplifying the slope properly, leading to incorrect answers.
AI-generated content may contain errors. Please verify critical information