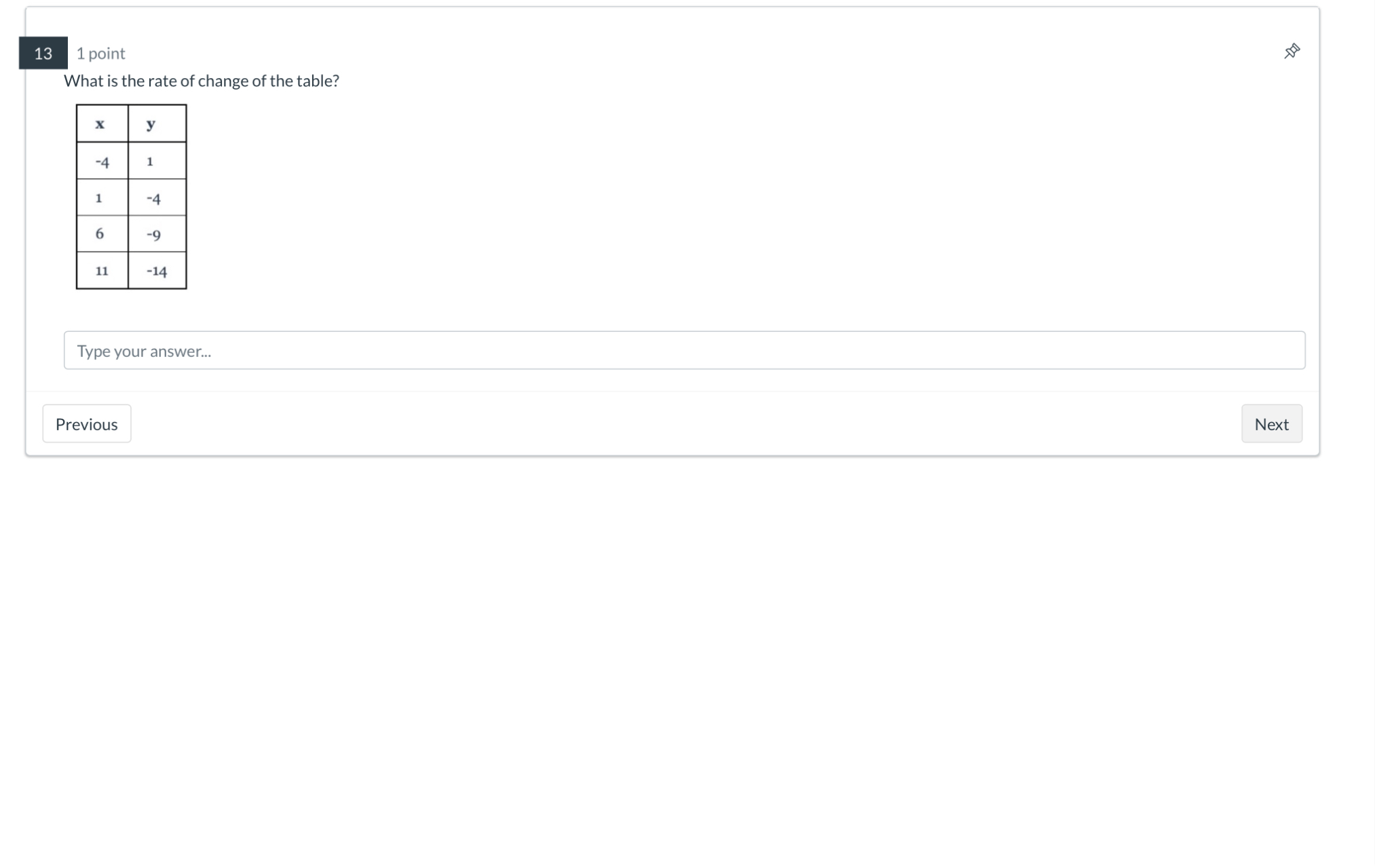
What is the rate of change of the table?

Understand the Problem

The question is asking for the rate of change based on the provided table of values for x and y. We need to determine how much y changes in relation to changes in x.

Answer

$-1$

Steps to Solve

Identify the change in y and x values
Calculate the change in ( y ) for each corresponding change in ( x ) using the formula:
$$ \text{Rate of Change} = \frac{\Delta y}{\Delta x} $$
For the pairs:

Between ( (-4, 1) ) and ( (1, -4) )
Between ( (1, -4) ) and ( (6, -9) )
Between ( (6, -9) ) and ( (11, -14) )

Calculate the rate of change for the first pair
For the points ( (-4, 1) ) and ( (1, -4) ):
$$ \Delta y = -4 - 1 = -5 $$
$$ \Delta x = 1 - (-4) = 5 $$
So,
$$ \text{Rate of Change} = \frac{-5}{5} = -1 $$
Calculate the rate of change for the second pair
For the points ( (1, -4) ) and ( (6, -9) ):
$$ \Delta y = -9 - (-4) = -5 $$
$$ \Delta x = 6 - 1 = 5 $$
So,
$$ \text{Rate of Change} = \frac{-5}{5} = -1 $$
Calculate the rate of change for the third pair
For the points ( (6, -9) ) and ( (11, -14) ):
$$ \Delta y = -14 - (-9) = -5 $$
$$ \Delta x = 11 - 6 = 5 $$
So,
$$ \text{Rate of Change} = \frac{-5}{5} = -1 $$
Conclusion
The rate of change is consistent across all intervals, which is:
$$ \text{Rate of Change} = -1 $$

The rate of change for the table is $-1$.

More Information

The rate of change being constant at $-1$ indicates that for every unit increase in ( x ), ( y ) decreases by 1 unit, showcasing a linear relationship.

Tips

Miscalculating the changes in ( x ) or ( y ).
Overlooking that the change should be calculated using the final minus the initial value.
Forgetting to check all pairs to confirm consistency.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!