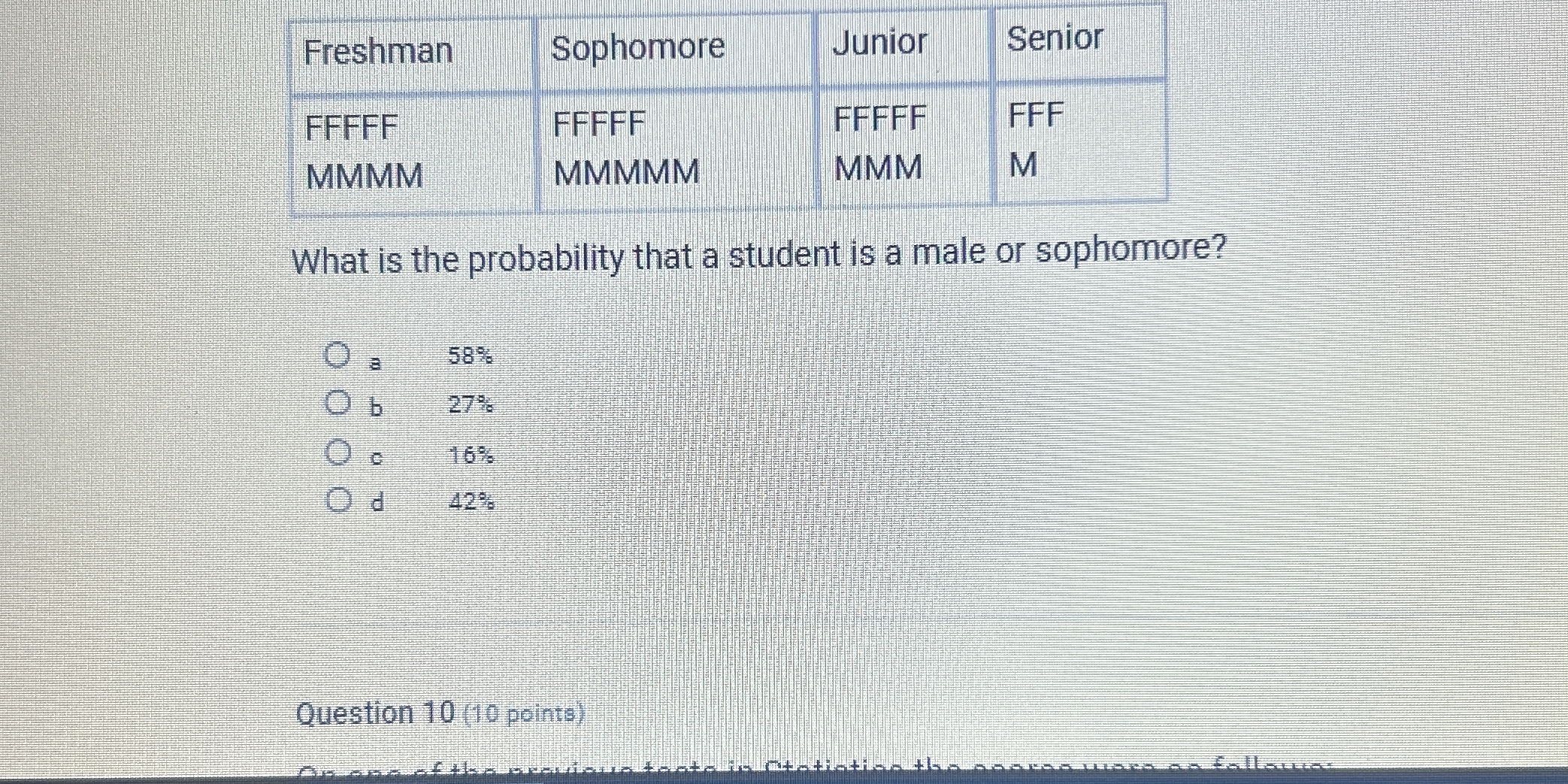
What is the probability that a student is a male or sophomore?
Understand the Problem
The question is asking for the probability that a randomly selected student is either a male or a sophomore, based on the given representations of gender within the different class years.
Answer
Approximately $61.54\%$
Answer for screen readers
The probability that a student is a male or sophomore is approximately $61.54%$.
Steps to Solve
- Count the Total Number of Students
We first need to determine the total number of students across all class years.
- Freshman: 4 F, 4 M → Total = 8
- Sophomore: 4 F, 4 M → Total = 8
- Junior: 4 F, 3 M → Total = 7
- Senior: 2 F, 1 M → Total = 3
Total number of students: $$ 8 + 8 + 7 + 3 = 26 $$
- Count the Number of Males
Next, we count the total number of males:
- Freshman: 4 M
- Sophomore: 4 M
- Junior: 3 M
- Senior: 1 M
Total number of males: $$ 4 + 4 + 3 + 1 = 12 $$
- Count the Number of Sophomores
Now, we count the total number of sophomores:
- Sophomore: 4 F + 4 M = 8
- Find the Total for Male or Sophomore using Inclusion-Exclusion Principle
To find the total number of students who are either male or sophomore, we need to use the inclusion-exclusion principle:
- Total either Male or Sophomore = Total males + Total sophomores - Total sophomores who are also male
Number of sophomores who are male:
- Sophomore: 4 M
Calculating: $$ 12 + 8 - 4 = 16 $$
- Calculate the Probability
Finally, the probability that a student chosen at random is either a male or a sophomore is given by the fraction of students who are male or sophomore to the total number of students: $$ P(\text{Male or Sophomore}) = \frac{16}{26} $$
This can be simplified to: $$ P(\text{Male or Sophomore}) = \frac{8}{13} \approx 0.6154 \text{ or } 61.54% $$
The probability that a student is a male or sophomore is approximately $61.54%$.
More Information
This probability indicates that there's a significant chance you will select a student who is either a male or in their sophomore year. It's a useful statistic in educational demographics.
Tips
- Forgetting to use the inclusion-exclusion principle: Many might just add the totals of males and sophomores without subtracting those that are counted twice (the males who are sophomores).
- Not simplifying the probability: Ensure you express the final answer as a percentage properly.
AI-generated content may contain errors. Please verify critical information