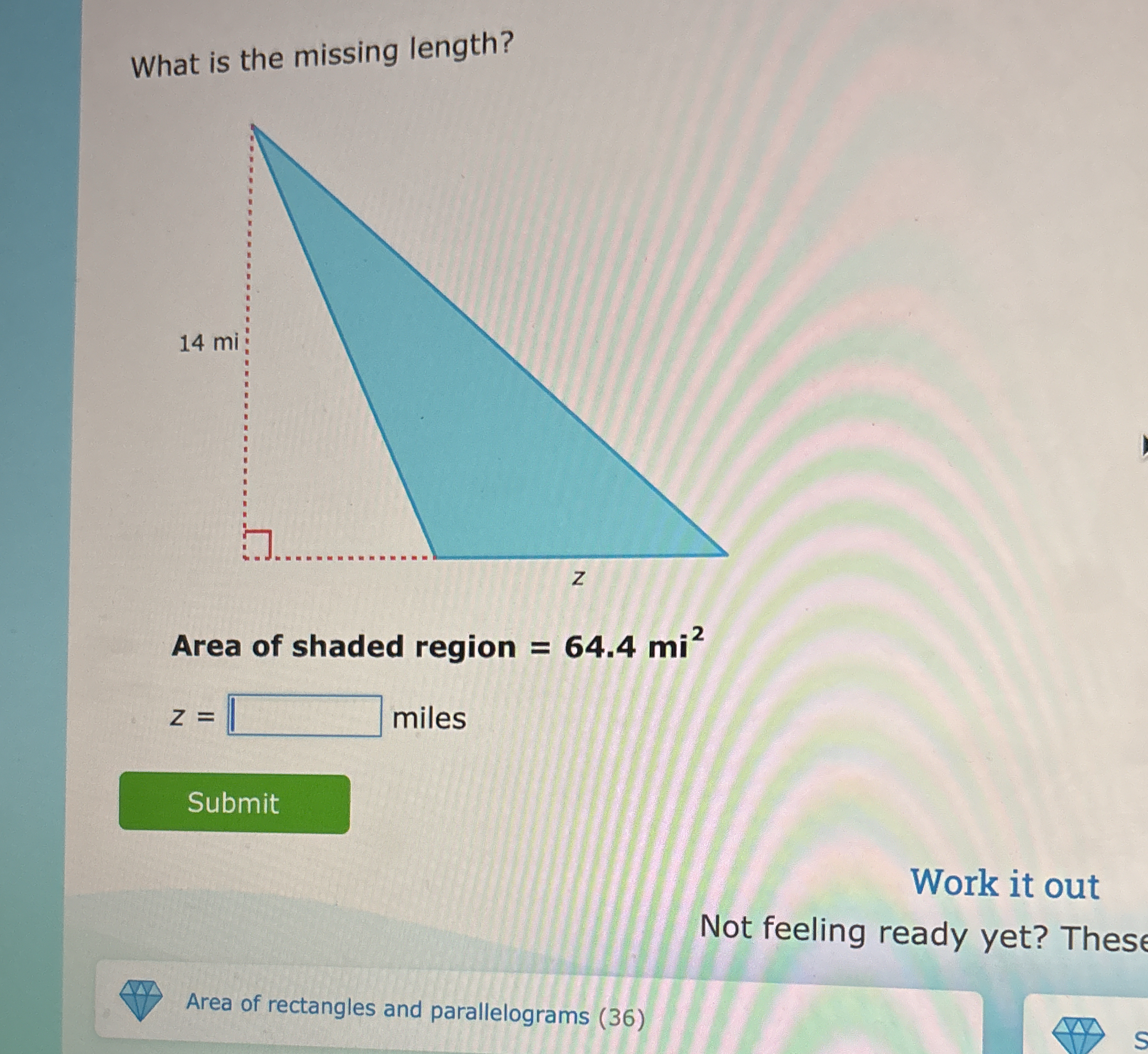
What is the missing length z in a triangle with a height of 14 miles and an area of 64.4 square miles?
Understand the Problem
The question is asking for the missing length 'z' of a triangle where the area of the shaded region is provided. To find 'z', we can use the formula for the area of a triangle, which is Area = 0.5 * base * height. Here, the height is given as 14 miles and the area is 64.4 square miles. We will rearrange the formula to solve for 'z'.
Answer
The missing length \( z \) is \( 9.2 \) miles.
Answer for screen readers
The missing length ( z ) is ( 9.2 ) miles.
Steps to Solve
- Identify the formula for the area of a triangle
The area ( A ) of a triangle can be calculated using the formula:
$$ A = \frac{1}{2} \times \text{base} \times \text{height} $$
- Plug in the known values
We know the area ( A = 64.4 ) square miles and the height ( h = 14 ) miles. Let's denote the base as ( z ). Replacing ( A ) and ( h ) in the formula gives us:
$$ 64.4 = \frac{1}{2} \times z \times 14 $$
- Rearrange the equation to solve for ( z )
Start by multiplying both sides of the equation by 2 to eliminate the fraction:
$$ 2 \times 64.4 = z \times 14 $$
So,
$$ 128.8 = z \times 14 $$
- Isolate ( z )
Now, divide both sides by 14 to solve for ( z ): $$ z = \frac{128.8}{14} $$
- Calculate the value of ( z )
Now compute the division: $$ z = 9.2 $$
The missing length ( z ) is ( 9.2 ) miles.
More Information
The calculation follows from a fundamental geometric principle where the area of a triangle is determined by its base and height. In this case, rearranging the area formula allows us to find the unknown base when the area and height are known.
Tips
- Forgetting to convert the units when necessary.
- Misplacing the height or base in the area formula.
- Mixing up the operations when rearranging equations.
AI-generated content may contain errors. Please verify critical information