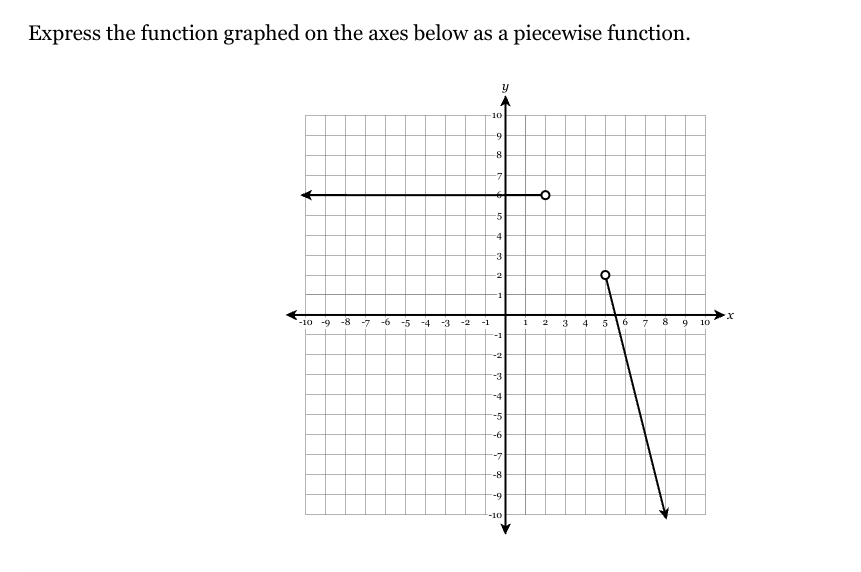
Express the function graphed on the axes below as a piecewise function.

Understand the Problem

The question is asking to express the function shown in the graph as a piecewise function, which involves analyzing the different segments of the graph and defining them with corresponding equations based on defined intervals.

Answer

$$ f(x) = \begin{cases} 6 & \text{for } -10 \leq x < 5 \\ -2x + 10 & \text{for } x \geq 5 \end{cases} $$

Steps to Solve

Identify graph segments and intervals

Looking at the graph, we have three distinct segments:

From $x = -10$ to $x = -1$, the function is constant at $y = 6$.
From $x = -1$ to $x = 5$, the function is also constant at $y = 6$ before it drops.
Finally, for $x \geq 5$, the function is linear and decreases to $y = -10$.

Define the piecewise function

Based on the segments identified, we can write the piecewise function as follows:

[ f(x) = \begin{cases} 6 & \text{for } -10 \leq x < 5 \ -2x + 10 & \text{for } x \geq 5 \end{cases} ]

Confirm function continuity

The graph shows that there is no gap between the segments, and the function is continuous at the transitions between intervals.

Complete piecewise function

Therefore, the complete piecewise function incorporating both identified equations and intervals is given above.

The piecewise function is:

$$ f(x) = \begin{cases} 6 & \text{for } -10 \leq x < 5 \ -2x + 10 & \text{for } x \geq 5 \end{cases} $$

More Information

This function represents a constant section followed by a linear decline. The function remains at $y = 6$ for the first segment, indicating there is no change in output within that interval, followed by a linear change that continues indefinitely.

Tips

Misidentifying the endpoints of the intervals, especially when they are open or closed.
Failing to note that the function can have constant values over an interval.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!