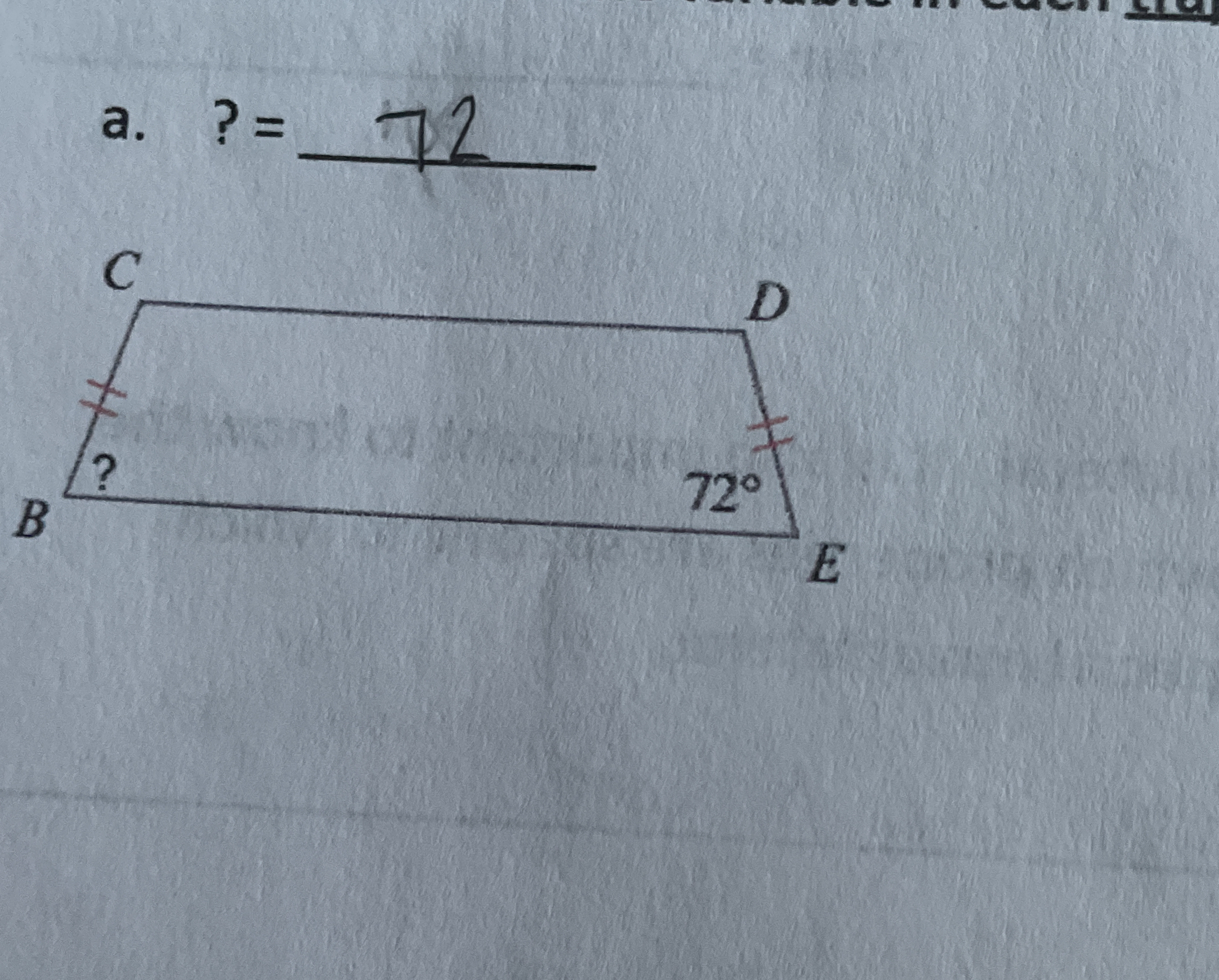
What is the missing angle in the trapezoid if one angle is 72 degrees?
Understand the Problem
The question is asking to find a missing angle in a trapezoid where one angle is provided as 72 degrees. We need to use the properties of trapezoids to determine the unknown angle.
Answer
The missing angle is $108^\circ$.
Answer for screen readers
The missing angle is $108^\circ$.
Steps to Solve
-
Identify the properties of a trapezoid In an isosceles trapezoid, the base angles are equal. This means that the angles on one side of the trapezoid are equal to the corresponding angles on the other side.
-
Set up the equation Given that one angle is $72^\circ$, we can denote the unknown angle as $x$. Since the trapezoid is isosceles, we have: $$ x = 72^\circ $$
-
Sum of angles in the trapezoid The sum of the interior angles of any quadrilateral, including trapezoids, is always $360^\circ$. Therefore, we can write the equation: $$ 72^\circ + 72^\circ + x + x = 360^\circ $$
-
Simplify the equation This can be simplified to: $$ 144^\circ + 2x = 360^\circ $$
-
Solve for x Now, isolate $x$: $$ 2x = 360^\circ - 144^\circ $$ $$ 2x = 216^\circ $$ $$ x = \frac{216^\circ}{2} $$ $$ x = 108^\circ $$
The missing angle is $108^\circ$.
More Information
Isosceles trapezoids have equal base angles, and the sum of all interior angles in a quadrilateral is $360^\circ$. Recognizing these properties is crucial for solving angle problems in trapezoids.
Tips
- Confusing the properties of isosceles trapezoids with those of other trapezoids.
- Forgetting to account for all angles when setting up the equation for the interior angles.
AI-generated content may contain errors. Please verify critical information