What is the length of segment C'C'? What is the length of segment B'C'?
Understand the Problem
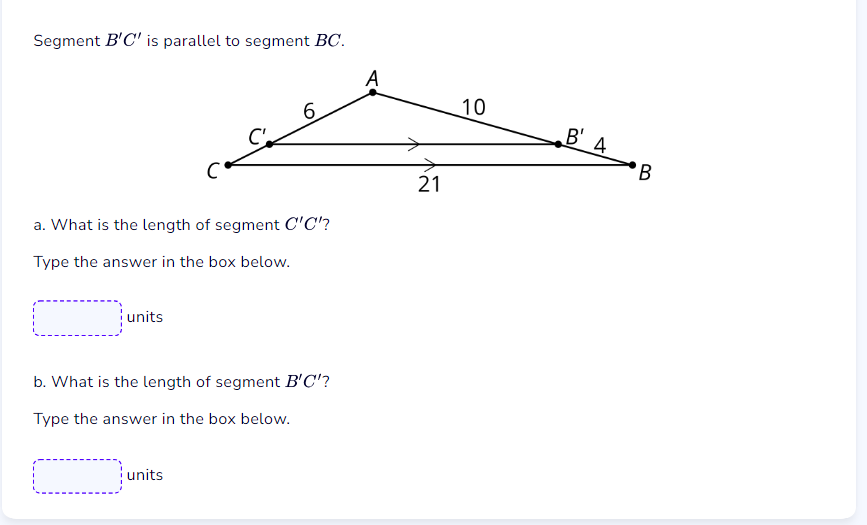
The question asks for the lengths of two segments, C'C' and B'C', in a geometric figure where one segment is parallel to another. To find these lengths, we likely need to apply the properties of similar triangles due to the parallel lines.
Answer
a. \(2.4\) units b. \(8.4\) units
Answer for screen readers
a. The length of segment (C'C') is (2.4) units.
b. The length of segment (B'C') is (8.4) units.
Steps to Solve
- Identify Proportions from Similar Triangles
Since segments $B'C'$ and $BC$ are parallel, triangles $AC'C$ and $AB'C$ are similar. This means the ratios of their corresponding sides are equal.
- Set Up Ratios
We know:
- The length of $C'A = 6$ units,
- The length of $AB' = 4$ units,
- The length of $AC = 10$ units,
- The length of $BC = 21$ units.
Thus, we can set up the following proportion to find $C'C'$:
$$ \frac{C'C'}{B'C} = \frac{C'A}{AB'} $$
Substituting the known lengths:
$$ \frac{C'C'}{4} = \frac{6}{10} $$
- Cross-Multiply to Solve for (C'C')
Cross-multiplying gives us:
$$ 10 C'C' = 24 $$
Now, we solve for $C'C'$:
$$ C'C' = \frac{24}{10} = 2.4 \text{ units} $$
- Find Length of Segment (B'C')
Next, we use the similar triangles again to find $B'C'$ using the ratio of the sides:
$$ \frac{B'C'}{BC} = \frac{AB'}{AC} $$
Substituting the known values:
$$ \frac{B'C'}{21} = \frac{4}{10} $$
- Cross-Multiply to Solve for (B'C')
Cross-multiplying gives us:
$$ 10 B'C' = 84 $$
Now, we solve for $B'C'$:
$$ B'C' = \frac{84}{10} = 8.4 \text{ units} $$
a. The length of segment (C'C') is (2.4) units.
b. The length of segment (B'C') is (8.4) units.
More Information
The relationships in similar triangles allow us to find lengths without needing to know every dimension. This method is widely used in geometry for various problems involving parallel lines and triangles.
Tips
- Not recognizing that the segments formed by parallel lines create similar triangles.
- Forgetting to set up the proportion correctly, which can lead to wrong values.
- Confusing the respective segments' lengths when substituting into ratios.
AI-generated content may contain errors. Please verify critical information