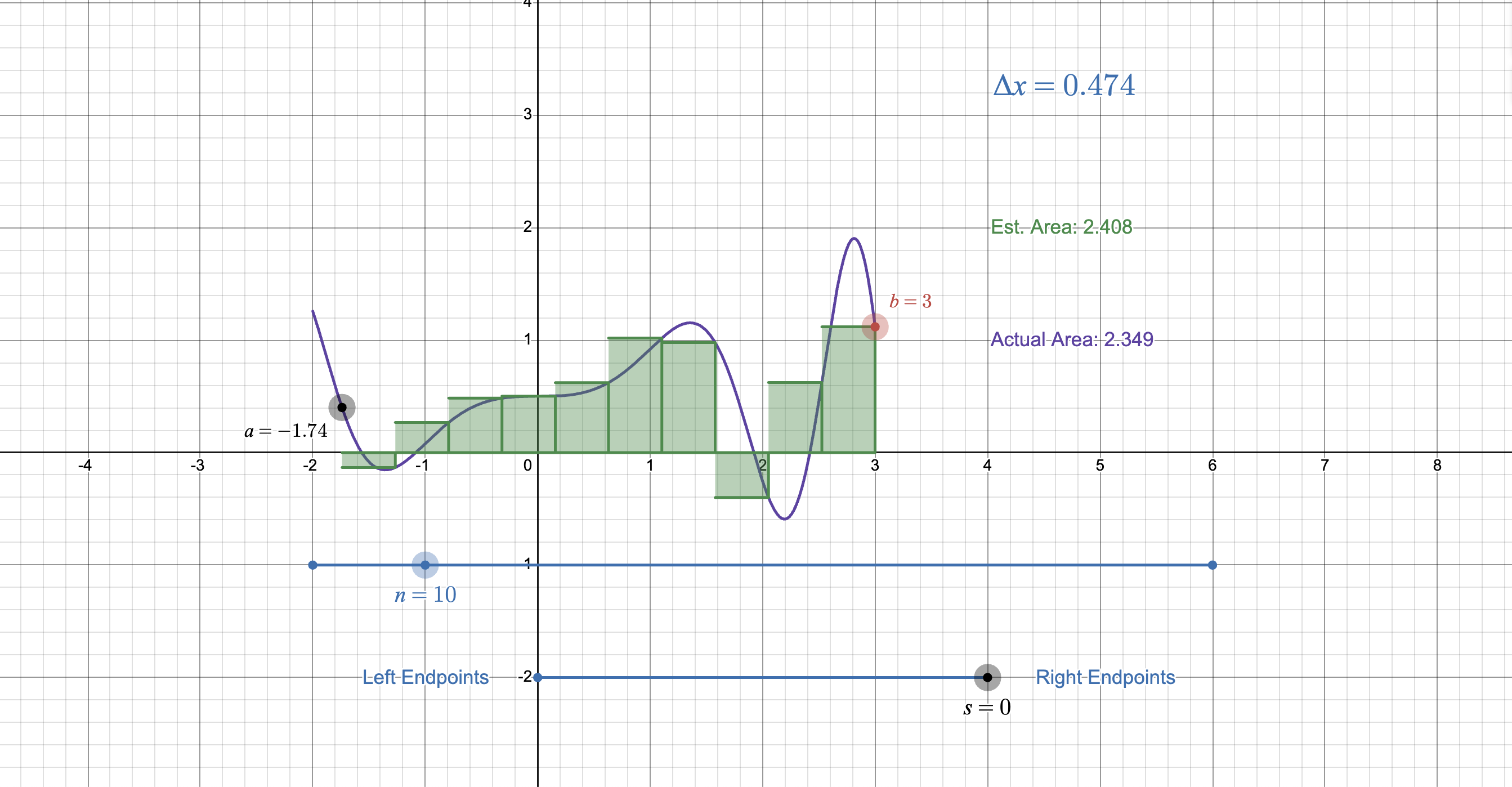
What is the estimated area and the actual area under the curve shown in the graph?

Steps to Solve

1. Identify the Interval and Number of Rectangles
   The interval for the function is given by $[a, b]$ where $a = -1.74$ and $b = 3$. The number of rectangles (subintervals) is $n = 10$.

2. Calculate the Width of Each Rectangle
   The width $\Delta x$ of each rectangle is calculated using the formula:
   $$ \Delta x = \frac{b - a}{n} $$
   Plugging in the values:
   $$ \Delta x = \frac{3 - (-1.74)}{10} = \frac{4.74}{10} = 0.474 $$

3. Determine the x-values for Left and Right Endpoints
   For left endpoints, the x-values are:
   $$ x_i = a + i \Delta x, \quad \text{for } i = 0, 1, 2, \ldots, n-1 $$
   For right endpoints, the x-values are:
   $$ x_i = a + (i+1) \Delta x, \quad \text{for } i = 0, 1, 2, \ldots, n $$

4. Estimate the Area Using Midpoint Rule
   The estimated area can be calculated using the midpoint of each rectangle. The formula for the estimated area is:
   $$ \text{Est. Area} = \Delta x \sum_{i=0}^{n-1} f(m_i) $$
   where $m_i$ is the midpoint of each rectangle.

5. Compare Estimated Area to Actual Area
   The actual area under the curve can be compared to the estimated area:
   $$ \text{Actual Area} = 2.349 \quad \text{(given)} $$
   The estimated area is 2.408.

6. Calculate the Error
   The error can be calculated as:
   $$ \text{Error} = |\text{Actual Area} - \text{Estimated Area}| $$
   Substituting the values:
   $$ \text{Error} = |2.349 - 2.408| = 0.059 $$