What is the next number in the sequence 10, 14, 25, 55, 140?
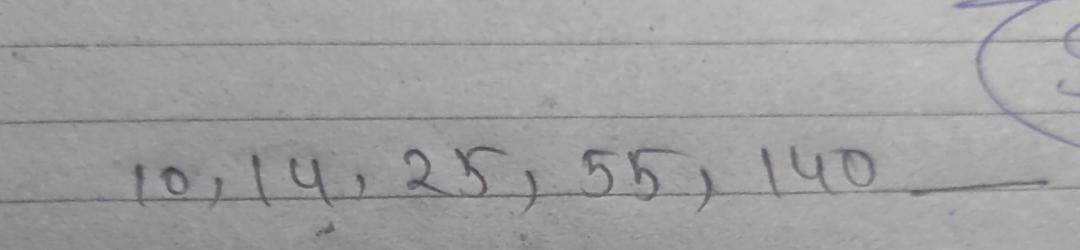
Understand the Problem
The question appears to present a sequence of numbers and may be asking for the next number in the sequence or a pattern analysis. Understanding the relationship between the numbers (10, 14, 25, 55, 140) will be key to determining how they are generated.
Answer
The next number in the sequence is $333$.
Answer for screen readers
The next number in the sequence is $333$.
Steps to Solve
- Identify the pattern in the sequence
Let's denote the sequence as:
$$ a_1 = 10, \quad a_2 = 14, \quad a_3 = 25, \quad a_4 = 55, \quad a_5 = 140 $$
We will look for a relationship between successive terms.
- Calculate the differences between the terms
Let's find the differences between consecutive terms:
$$ a_2 - a_1 = 14 - 10 = 4 $$
$$ a_3 - a_2 = 25 - 14 = 11 $$
$$ a_4 - a_3 = 55 - 25 = 30 $$
$$ a_5 - a_4 = 140 - 55 = 85 $$
So we have the first differences:
$$ 4, 11, 30, 85 $$
- Calculate the second differences
Next, we find the differences of the first differences:
$$ 11 - 4 = 7 $$
$$ 30 - 11 = 19 $$
$$ 85 - 30 = 55 $$
So, the second differences are:
$$ 7, 19, 55 $$
- Calculate the third differences
Now, we find the differences of the second differences:
$$ 19 - 7 = 12 $$
$$ 55 - 19 = 36 $$
So, the third differences are:
$$ 12, 36 $$
- Identify a polynomial pattern
The pattern of differences suggests we may be dealing with a polynomial. The third differences are not constant, but they may continue to increase geometrically or arithmetically.
- Predict the next difference
If we examine the last difference ($36$) and consider a polynomial behavior, we can predict the next difference in a similar increasing manner. Assume the constant increase in third differences leads us to estimate the next term of the sequence.
Continuing the sequence of third differences, we guess:
$$ 12, 36, \text{(next)} = 108 $$
- Calculate the next number in the sequence
Thus, we can find the next first difference:
$$ 85 + 108 = 193 $$
Now, add this new difference to the last term of the original sequence:
$$ 140 + 193 = 333 $$
The next number in the sequence is $333$.
More Information
This sequence seems to involve successive differences leading to a polynomial function. The process of calculating differences is a common method for identifying patterns in numeric sequences.
Tips
- Not calculating the differences correctly. Always double-check each subtraction to ensure accuracy.
- Assuming a linear pattern too quickly; make sure to check higher-order differences.
AI-generated content may contain errors. Please verify critical information