What is the equation of the line?
Understand the Problem
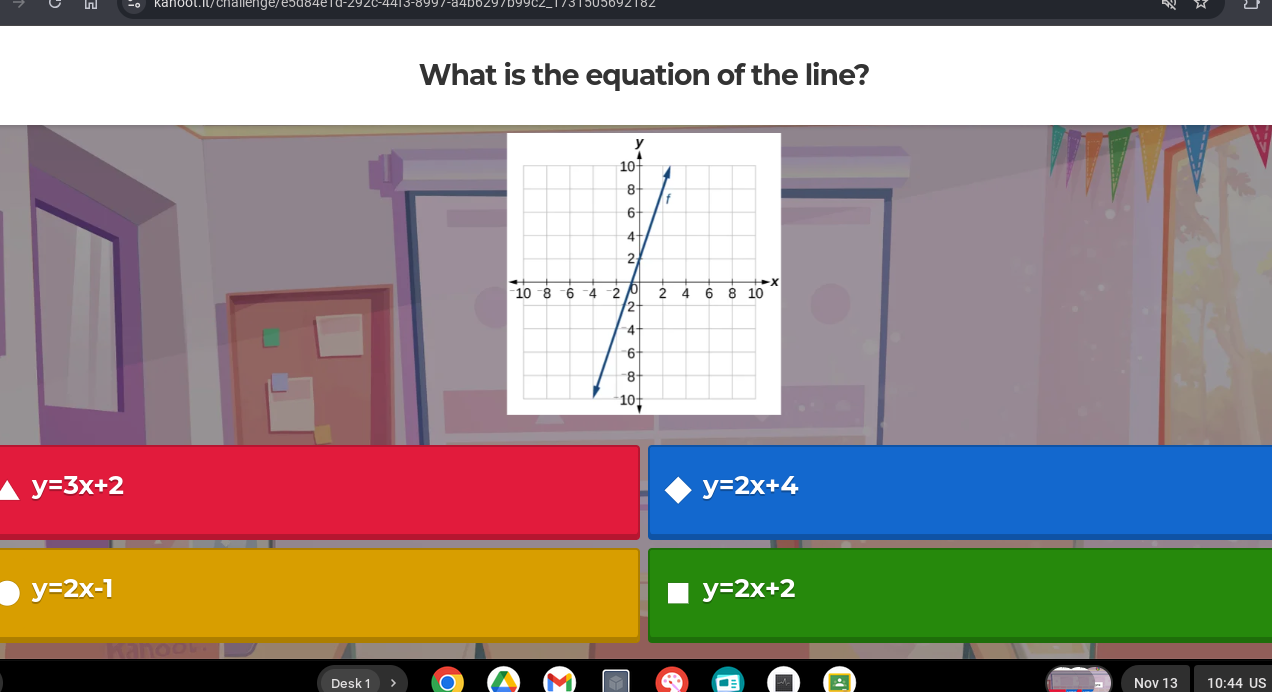
The question is asking for the equation of the line represented in the graph. The equation can typically be determined by identifying the slope and the y-intercept from the graph provided.
Answer
The equation is $y = 2x + 2$.
Answer for screen readers
The equation of the line is $y = 2x + 2$.
Steps to Solve
- Identify the y-intercept
The y-intercept is the point where the line crosses the y-axis. From the graph, the line seems to intersect the y-axis at $y = 2$. Thus, the y-intercept is 2.
- Determine the slope
To find the slope (m), pick two points from the line. For example, let's choose the points (0, 2) and (2, 6).
The formula for the slope is:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
Substituting the chosen points:
$$ m = \frac{6 - 2}{2 - 0} = \frac{4}{2} = 2 $$
- Write the equation of the line
The equation of a line in slope-intercept form is given by:
$$ y = mx + b $$
We have found $m = 2$ and $b = 2$. Plugging in these values, the equation of the line is:
$$ y = 2x + 2 $$
The equation of the line is $y = 2x + 2$.
More Information
This equation indicates that for every unit increase in $x$, $y$ increases by 2 units, and the line crosses the y-axis at (0,2).
Tips
- Forgetting to simplify the slope or y-intercept accurately can lead to wrong equations.
- Misreading the graph to identify the wrong intersection points can yield incorrect slopes.
AI-generated content may contain errors. Please verify critical information