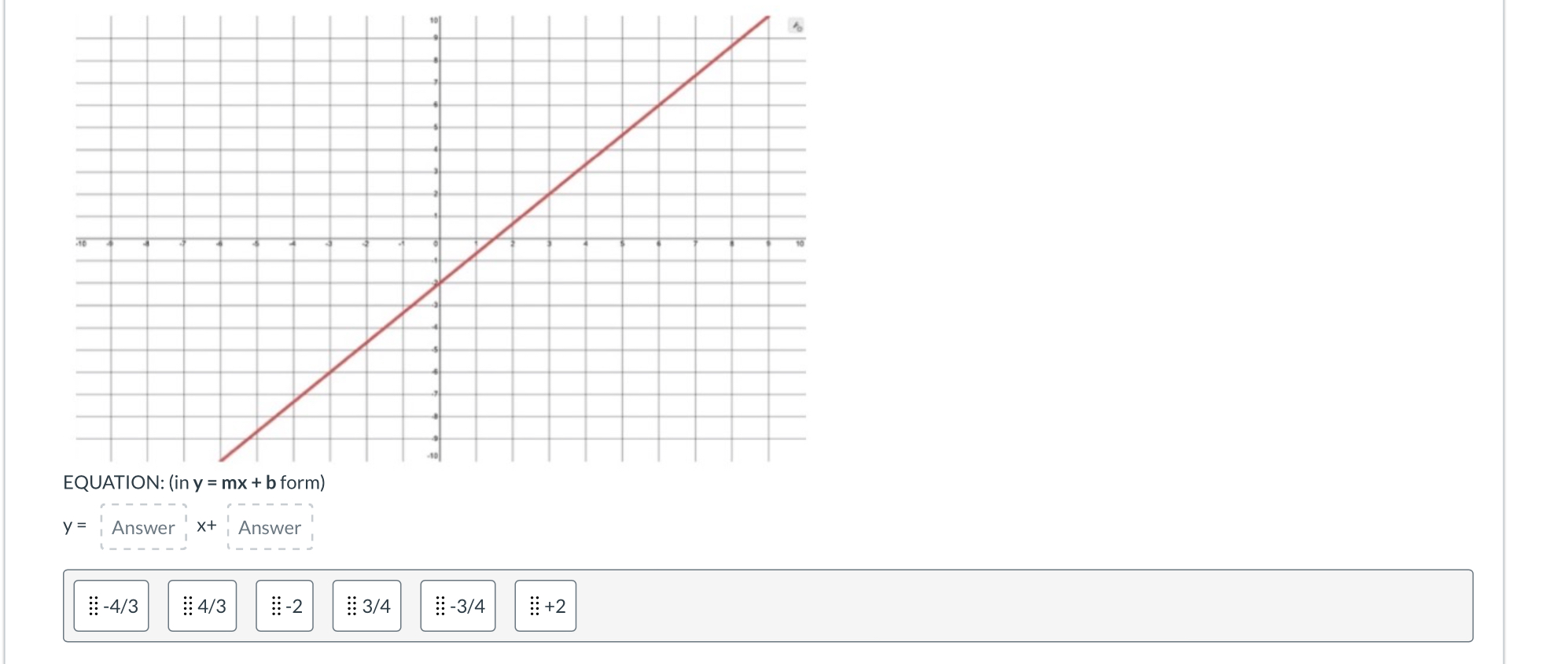
What is the equation in y = mx + b form based on the provided graph?
Understand the Problem
The question is asking for the equation of a line in slope-intercept form (y = mx + b) based on a given graph. We need to identify the slope (m) and the y-intercept (b) from the graph to formulate the equation.
Answer
The equation of the line is \( y = x + 2 \).
Answer for screen readers
The equation of the line is ( y = x + 2 ).
Steps to Solve
- Identify the Y-Intercept (b)
From the graph, observe where the line crosses the y-axis. This point gives us the value of $b$. In this case, the line crosses at ( y = 2 ), so ( b = 2 ).
- Determine the Slope (m)
Next, find two clear points on the line to calculate the slope. For example, using the points ((0, 2)) and ((3, 5)):
- The formula for slope is given by:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
- Plugging in our points:
$$ m = \frac{5 - 2}{3 - 0} = \frac{3}{3} = 1 $$
- Write the Equation
Now that we have the slope ( m = 1 ) and the y-intercept ( b = 2 ), we can write the equation of the line in slope-intercept form:
$$ y = mx + b $$
Substituting our values:
$$ y = 1x + 2 $$
Thus, the equation simplifies to:
$$ y = x + 2 $$
The equation of the line is ( y = x + 2 ).
More Information
The slope-intercept form of a line is useful for quickly identifying the slope and y-intercept directly from the equation. The slope ( m ) indicates the steepness and direction of the line, while the y-intercept ( b ) shows where the line crosses the y-axis.
Tips
- Mistaking the slope: Be careful to count the rise and run correctly when identifying the slope from the graph.
- Misreading the y-intercept: Ensure you correctly identify the point where the line crosses the y-axis.
AI-generated content may contain errors. Please verify critical information