What is the definition of the Riemann zeta function?
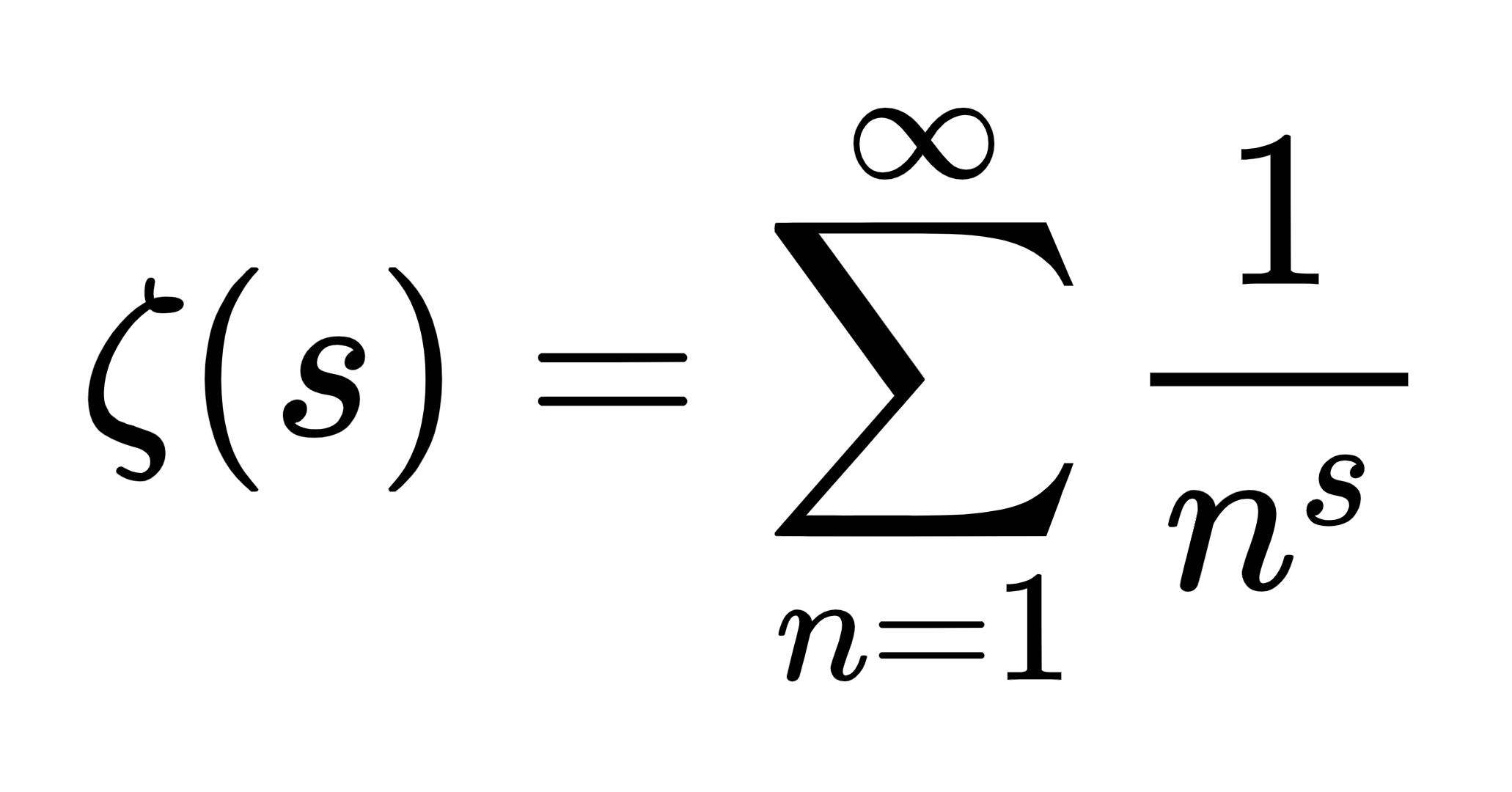
Understand the Problem
The image presents the mathematical definition of the Riemann zeta function, which is defined as the sum of the series 1/n^s for n from 1 to infinity. It represents a fundamental function in number theory and has implications in various areas such as complex analysis and harmonic series.
Answer
The Riemann zeta function is defined as \( \zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s} \) and converges for \( s > 1 \).
Answer for screen readers
The Riemann zeta function is defined as:
$$ \zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s} $$
It converges for ( s > 1 ).
Steps to Solve
- Definition of the Riemann zeta function The Riemann zeta function is defined as:
$$ \zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s} $$
Where ( s ) is a complex number.
-
Understanding the series The series ( \sum_{n=1}^{\infty} \frac{1}{n^s} ) represents an infinite sum. If ( s ) is greater than 1, this series converges to a specific value. If ( s \leq 1 ), the series diverges.
-
Convergence conditions For convergence, we state:
- The series converges for ( s > 1 ).
- The series diverges for ( s \leq 1 ).
- Example for convergence For ( s = 2 ):
$$ \zeta(2) = \sum_{n=1}^{\infty} \frac{1}{n^2} $$
This series converges to ( \frac{\pi^2}{6} ).
- Calculating a specific value For another example, if we calculate ( \zeta(3) ):
$$ \zeta(3) = \sum_{n=1}^{\infty} \frac{1}{n^3} $$
This value is known to be approximately ( 1.2020569 ).
The Riemann zeta function is defined as:
$$ \zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s} $$
It converges for ( s > 1 ).
More Information
The Riemann zeta function plays a crucial role in number theory, particularly in understanding the distribution of prime numbers. The function extends to complex numbers and has applications in various fields including physics and probability.
Tips
- Not recognizing the convergence requirements: Remember that the series only converges for ( s > 1 ).
- Misinterpreting the value of ( s ): Ensure you check the value of ( s ) before making calculations about convergence.
AI-generated content may contain errors. Please verify critical information