What is the Collatz Conjecture and how is the function f(n) defined for even and odd integers?
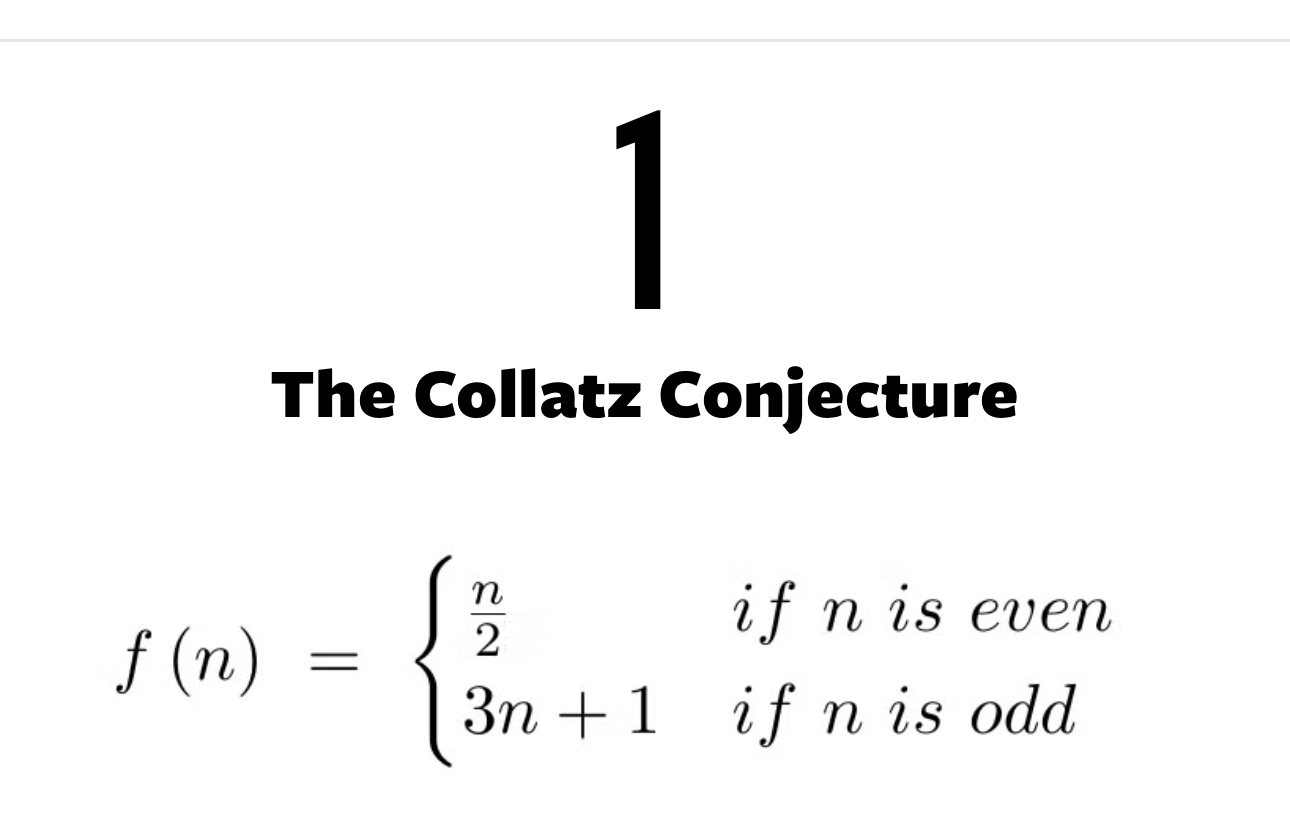
Understand the Problem
The question is presenting the Collatz Conjecture, which defines a function f(n) for integers based on whether they are even or odd. It describes how to transform each integer n into another integer using specific rules, leading to inquiries about the properties or results of this function.
Answer
The sequence for $n = 6$ is $6 \to 3 \to 10 \to 5 \to 16 \to 8 \to 4 \to 2 \to 1$.
Answer for screen readers
For the starting integer $n = 6$, the sequence generated by the function $f(n)$ is:
$$ 6 \to 3 \to 10 \to 5 \to 16 \to 8 \to 4 \to 2 \to 1 $$
Steps to Solve
-
Define the function based on parity
The function $f(n)$ is defined as follows:
- If $n$ is even: $$ f(n) = \frac{n}{2} $$
- If $n$ is odd: $$ f(n) = 3n + 1 $$
-
Choose a starting integer
To explore the Collatz Conjecture, choose a starting integer $n$. For example, let’s take $n = 6$.
-
Apply the function iteratively
Start applying the function iteratively based on whether the current value of $n$ is even or odd:
- For $n = 6$ (even): $$ f(6) = \frac{6}{2} = 3 $$
- For $n = 3$ (odd): $$ f(3) = 3(3) + 1 = 10 $$
- For $n = 10$ (even): $$ f(10) = \frac{10}{2} = 5 $$
- For $n = 5$ (odd): $$ f(5) = 3(5) + 1 = 16 $$
- For $n = 16$ (even): $$ f(16) = \frac{16}{2} = 8 $$
- For $n = 8$ (even): $$ f(8) = \frac{8}{2} = 4 $$
- For $n = 4$ (even): $$ f(4) = \frac{4}{2} = 2 $$
- For $n = 2$ (even): $$ f(2) = \frac{2}{2} = 1 $$
- For $n = 1$ (odd): $$ f(1) = 3(1) + 1 = 4 $$
-
Identify the cycle
Continue iterating until you reach 1, which will lead to a repeating cycle (1 \to 4 \to 2 \to 1).
For the starting integer $n = 6$, the sequence generated by the function $f(n)$ is:
$$ 6 \to 3 \to 10 \to 5 \to 16 \to 8 \to 4 \to 2 \to 1 $$
More Information
The Collatz Conjecture suggests that no matter which positive integer you start with, you will eventually reach 1, leading to a repeating cycle of 1, 4, 2, and back to 1. This conjecture remains unproven despite extensive computational evidence.
Tips
- Not applying the rules correctly: Ensure to check the parity (even or odd) of the current number before applying the function.
- Forgetting to continue until reaching 1: Some may stop prematurely; the goal is to continue the iterations fully until reaching the number 1.
AI-generated content may contain errors. Please verify critical information