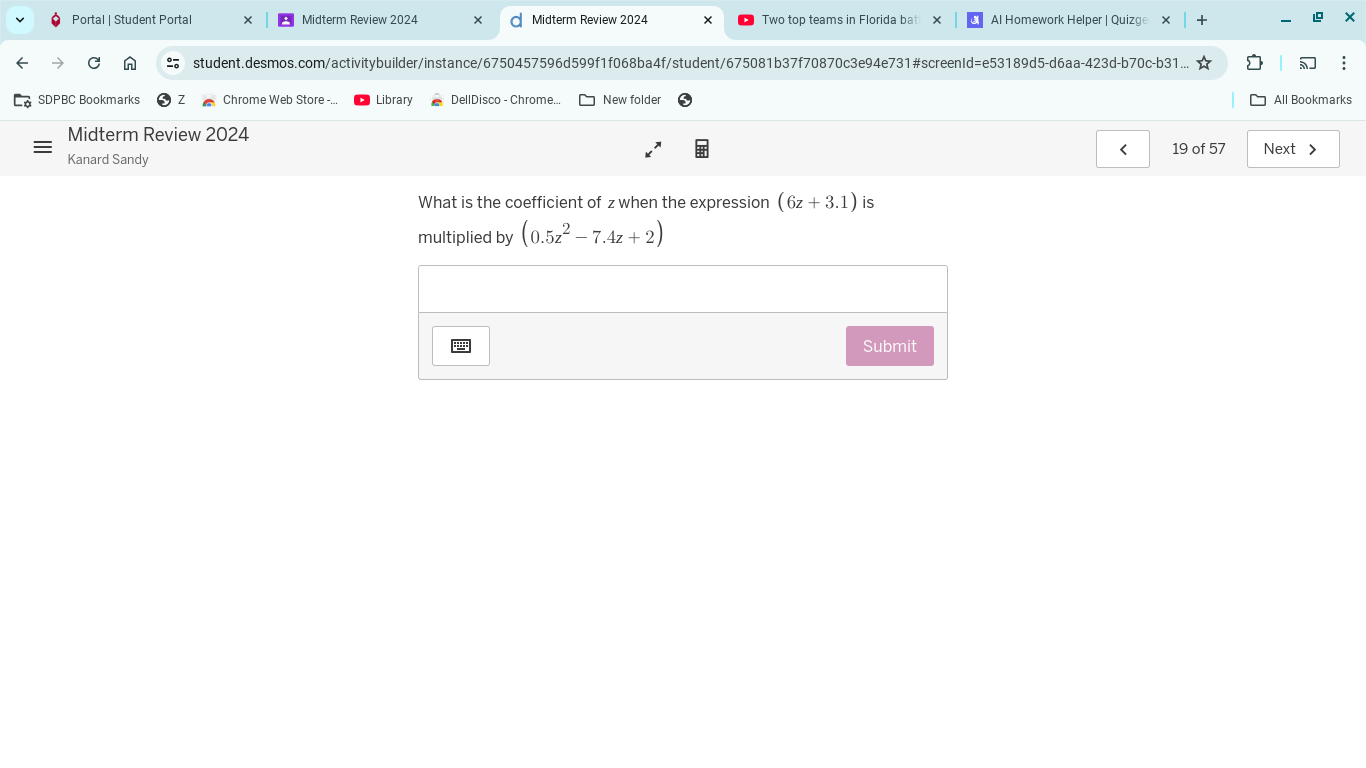
What is the coefficient of z when the expression (6z + 3.1) is multiplied by (0.5z^2 - 7.4z + 2)?

Understand the Problem

The question is asking to find the coefficient of z in a product of two algebraic expressions. This involves multiplying the expressions and then identifying the coefficient of the z term from the resulting expression.

Answer

The coefficient of $z$ is $-10.94$.

Steps to Solve

Identify the expressions to multiply

We need to multiply the expressions ( (6z + 3.1) ) and ( (0.5z^2 - 7.4z + 2) ).

Distribute the first expression

Use the distributive property (also known as the FOIL method for binomials) to multiply each term in the first expression by each term in the second expression.

[ (6z)(0.5z^2) + (6z)(-7.4z) + (6z)(2) + (3.1)(0.5z^2) + (3.1)(-7.4z) + (3.1)(2) ]

Calculate each multiplication

Now we multiply the terms:

( 6z \cdot 0.5z^2 = 3z^3 )
( 6z \cdot (-7.4z) = -44.4z^2 )
( 6z \cdot 2 = 12z )
( 3.1 \cdot 0.5z^2 = 1.55z^2 )
( 3.1 \cdot (-7.4z) = -22.94z )
( 3.1 \cdot 2 = 6.2 )

Combine like terms

Now we combine the results to find the final expression:

[ 3z^3 + (-44.4z^2 + 1.55z^2) + (12z - 22.94z) + 6.2 ]

This simplifies to:

[ 3z^3 - 42.85z^2 - 10.94z + 6.2 ]

The coefficient of ( z ) is ( -10.94 ).

The coefficient of ( z ) is $-10.94$.

More Information

The problem involves polynomial multiplication and combining like terms. The coefficient represents how many units of ( z ) are in the resulting expression.

Tips

Forgetting to distribute each term properly and missing some products.
Not combining like terms correctly, which can lead to an incorrect coefficient.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!