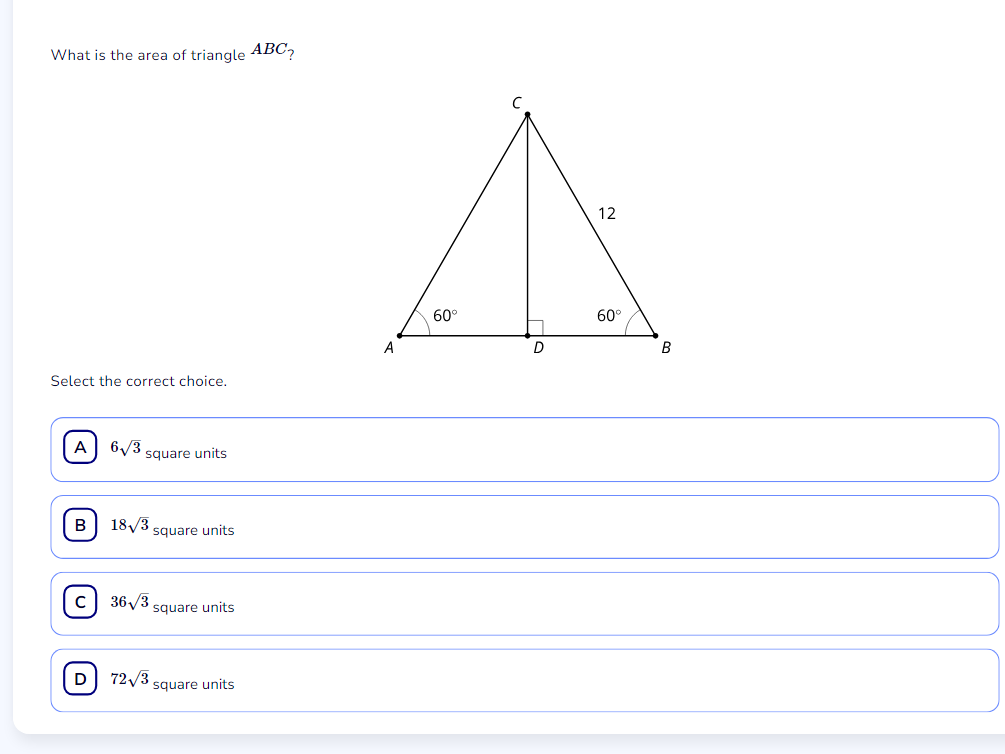
What is the area of triangle ABC?

Understand the Problem

The question is asking for the area of triangle ABC, providing measurements and angles to calculate the area using geometry. The area can be found using the formula for the area of a triangle, given the base and height or using trigonometric relationships.

Answer

The area of triangle ABC is $ 48\sqrt{3} $ square units.

Steps to Solve

Identify Relevant Information

From the triangle ABC, we know that angle $A = 60^\circ$, the height $CD = 12$, and since angle $C$ is directly above point $D$, triangle $ACD$ can be analyzed.

Determine Side AC

Using the sine function, we can relate the angle and the opposite side to find the base $AD$. The sine of angle $A$ gives us: $$ \sin(A) = \frac{CD}{AC} $$

Substituting the values, we get: $$ \sin(60^\circ) = \frac{12}{AC} $$

Since $\sin(60^\circ) = \frac{\sqrt{3}}{2}$, we can now solve for ( AC ): $$ \frac{\sqrt{3}}{2} = \frac{12}{AC} $$

Solve for AC

Rearranging the equation gives: $$ AC = \frac{12 \cdot 2}{\sqrt{3}} = \frac{24}{\sqrt{3}} = 8\sqrt{3} $$

Calculate Area of Triangle ABC

The area $A$ of triangle ABC can be calculated using the formula: $$ A = \frac{1}{2} \times \text{base} \times \text{height} $$ Substituting ( AD = AC ) (which we calculated) and the height ( CD = 12 ): $$ A = \frac{1}{2} \times 8\sqrt{3} \times 12 $$

Final Area Calculation

Calculating this gives: $$ A = \frac{1}{2} \times 96\sqrt{3} = 48\sqrt{3} $$

The area of triangle ABC is ( 48\sqrt{3} ) square units.

More Information

The area calculated uses basic trigonometric principles along with the area formula for a triangle. It's useful to know that angle measures and heights are critical in these calculations.

Tips

Misunderstanding the orientation of angles can lead to incorrect sine or cosine usage.
Forgetting to multiply by ( \frac{1}{2} ) in the area formula is a frequent error.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!