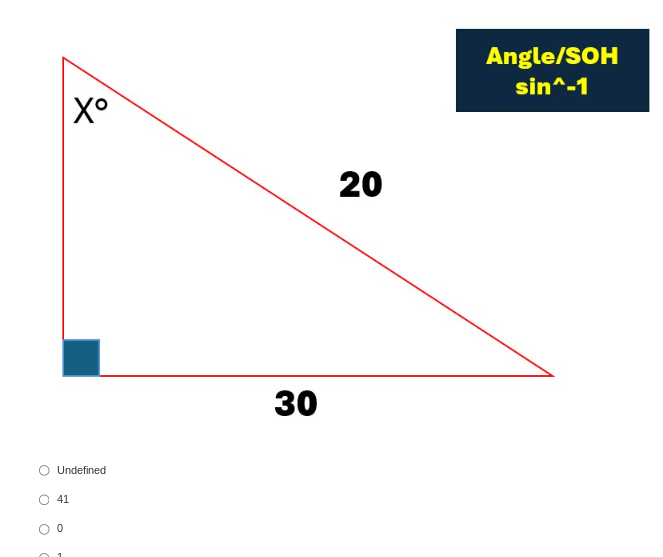
What is the angle X° in a right triangle with an opposite side of 20 and a hypotenuse of 30?
Understand the Problem
The question is asking to find the angle X° in a right triangle given the lengths of the opposite side (20) and the hypotenuse (30). We will use the sine function and its inverse to determine the angle.
Answer
The angle is approximately $42°$.
Answer for screen readers
The angle ( X ) is approximately ( 42° ).
Steps to Solve
-
Identify the sine function The sine function is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle. Therefore, we can express this as: $$ \sin(X) = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{20}{30} $$
-
Simplify the sine ratio We can simplify the fraction: $$ \frac{20}{30} = \frac{2}{3} $$ So, we have: $$ \sin(X) = \frac{2}{3} $$
-
Use the inverse sine function To find the angle ( X ), we use the inverse sine function: $$ X = \sin^{-1}\left(\frac{2}{3}\right) $$
-
Calculate the angle Using a calculator, we can find: $$ X \approx 41.81° $$ Rounding to the nearest whole number gives: $$ X \approx 42° $$
The angle ( X ) is approximately ( 42° ).
More Information
The sine function is fundamental in trigonometry, relating the angles of a right triangle to the ratios of its sides. The inverse sine function ((\sin^{-1})) allows us to find an angle when given the lengths of sides.
Tips
- Forgetting to simplify the ratio before using the inverse sine function.
- Using the calculator in the wrong mode (degrees vs radians) when finding the angle.
AI-generated content may contain errors. Please verify critical information