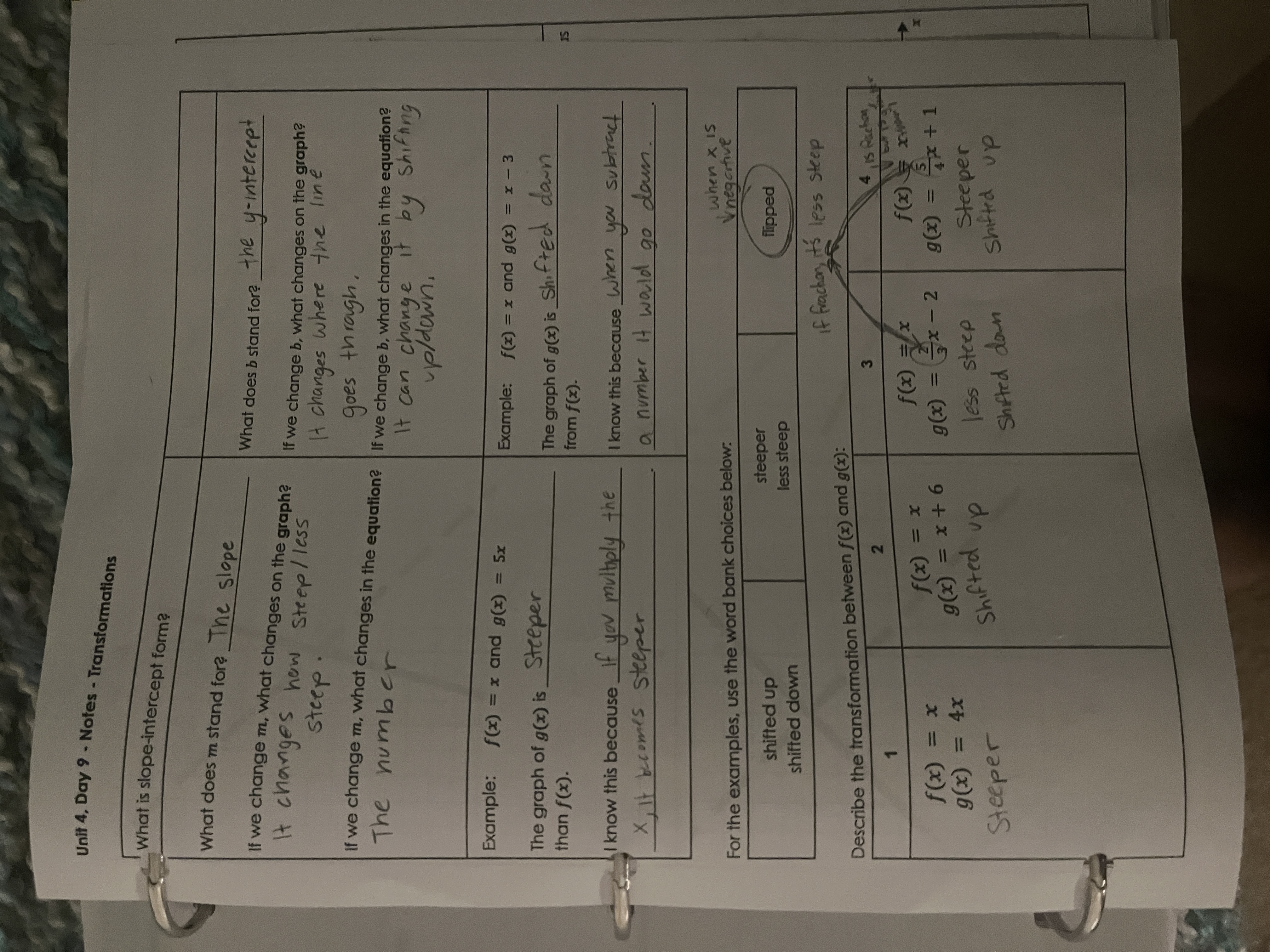
What is slope-intercept form? What do m and b stand for? How do changes to m and b affect the graph and equation? Describe the transformation between the given functions.
Understand the Problem
The question relates to understanding slope-intercept form in linear equations, exploring how changes in the slope (m) and y-intercept (b) affect the graph and the equation of lines. It involves identifying transformations between functions based on the slope and shifts.
Answer
1. Steeper 2. Shifted up 3. Less steep 4. Steeper
Answer for screen readers
- The transformation between $f(x) = x$ and $g(x) = 4x$ is that $g(x)$ is steeper.
- The transformation between $f(x) = x$ and $g(x) = x + 6$ is that $g(x)$ is shifted up.
- The transformation between $f(x) = x$ and $g(x) = \frac{1}{2}x$ is that $g(x)$ is less steep.
- The transformation between $f(x) = \frac{1}{2}x$ and $g(x) = \frac{5}{4}x + 1$ is that $g(x)$ is steeper (compared to $f(x)$, given the slope is increased).
Steps to Solve
- Identifying the Slope (m) and y-Intercept (b)
In slope-intercept form, the equation of a line is given by $y = mx + b$ where $m$ is the slope and $b$ is the y-intercept. The slope determines how steep the line is.
- Understanding Changes in m
If we change the slope $m$, it affects the steepness of the line.
- If $m$ becomes larger (more positive or less negative), the line becomes steeper.
- If $m$ becomes smaller (more negative or less positive), the line becomes less steep.
For example, if $f(x) = x$ and $g(x) = 4x$, since $4$ is greater than $1$, $g(x)$ is steeper.
- Understanding Changes in b
If we change the y-intercept $b$, it affects where the line crosses the y-axis.
- If $b$ increases, the line shifts up.
- If $b$ decreases, the line shifts down.
For instance, if $f(x) = x$ and $g(x) = x + 6$, the line is shifted up by 6 units.
- Describing Transformations Between Functions
When comparing two functions, we need to analyze how their slopes and y-intercepts differ.
- Example 1: $f(x) = x$ and $g(x) = 4x$ indicates that $g(x)$ is steeper than $f(x)$.
- Example 2: $f(x) = x$ and $g(x) = x + 6$ shows that $g(x)$ is the same steepness but shifted up.
- Example 3: $f(x) = x$ and $g(x) = \frac{1}{2}x$ indicates that $g(x)$ is less steep due to the smaller slope.
- The transformation between $f(x) = x$ and $g(x) = 4x$ is that $g(x)$ is steeper.
- The transformation between $f(x) = x$ and $g(x) = x + 6$ is that $g(x)$ is shifted up.
- The transformation between $f(x) = x$ and $g(x) = \frac{1}{2}x$ is that $g(x)$ is less steep.
- The transformation between $f(x) = \frac{1}{2}x$ and $g(x) = \frac{5}{4}x + 1$ is that $g(x)$ is steeper (compared to $f(x)$, given the slope is increased).
More Information
The slope-intercept form is especially useful in algebra for understanding linear relationships. The effects of changing the slope and y-intercept help visualize how lines shift on a graph. A steeper line corresponds to a greater absolute value of the slope, while the y-intercept alters the position of the line without changing its angle.
Tips
- Confusing slope and y-intercept: Students often mix up how changes in $m$ affect the steepness versus how changes in $b$ affect the position on the y-axis. To avoid this, remember that $m$ controls the angle and $b$ controls the starting point.
- Forgetting that negative slopes can still be steep: When dealing with negative slopes, a larger negative number (e.g., $-4$) is steeper than a smaller negative number (e.g., $-1$).
AI-generated content may contain errors. Please verify critical information