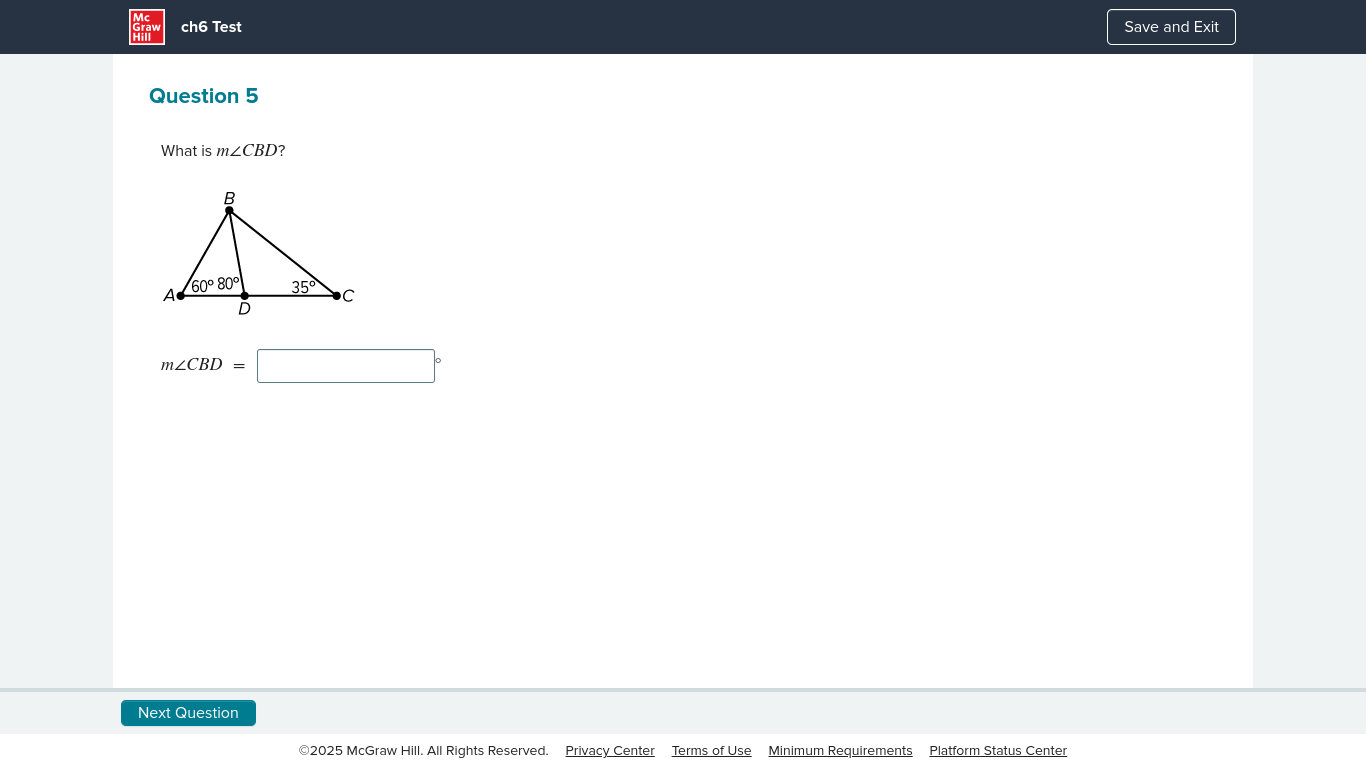
What is m∠CBD?
Understand the Problem
The question is asking for the measurement of angle CBD in a triangle where angle ABD is given as 60° and angle ACD as 35°. We will find this measurement using the properties of angles in a triangle.
Answer
The measure of angle \( CBD \) is \( 85^\circ \).
Answer for screen readers
The measure of angle ( CBD ) is ( 85^\circ ).
Steps to Solve
- Identify given angles
We have the following angles provided in the triangle:
- Angle ( ABD = 60^\circ )
- Angle ( ACD = 35^\circ )
- Determine angle ADB
Since angle ( ADB ) is vertically opposite angle ( ACD ), we can conclude that:
$$ m\angle ADB = 35^\circ $$
- Apply the triangle angle sum property
The sum of the angles in triangle ( ABD ) must equal ( 180^\circ ). Therefore, we can express this as:
$$ m\angle ABD + m\angle ADB + m\angle CBD = 180^\circ $$
Substituting the known values:
$$ 60^\circ + 35^\circ + m\angle CBD = 180^\circ $$
- Solve for angle CBD
Now we can solve for ( m\angle CBD ):
$$ m\angle CBD = 180^\circ - (60^\circ + 35^\circ) $$
Calculating the right-hand side:
$$ m\angle CBD = 180^\circ - 95^\circ = 85^\circ $$
The measure of angle ( CBD ) is ( 85^\circ ).
More Information
In triangle geometry, the angle sum property states that the sum of the interior angles in a triangle will always equal ( 180^\circ ). This concept is fundamental in solving problems involving triangles.
Tips
- Forgetting that the angles add up to ( 180^\circ ): Always remember the triangle angle sum property.
- Confusing which angles are vertically opposite: Ensure to correctly identify which angles correspond to each other.
AI-generated content may contain errors. Please verify critical information