What is 9/7 + 7/13?
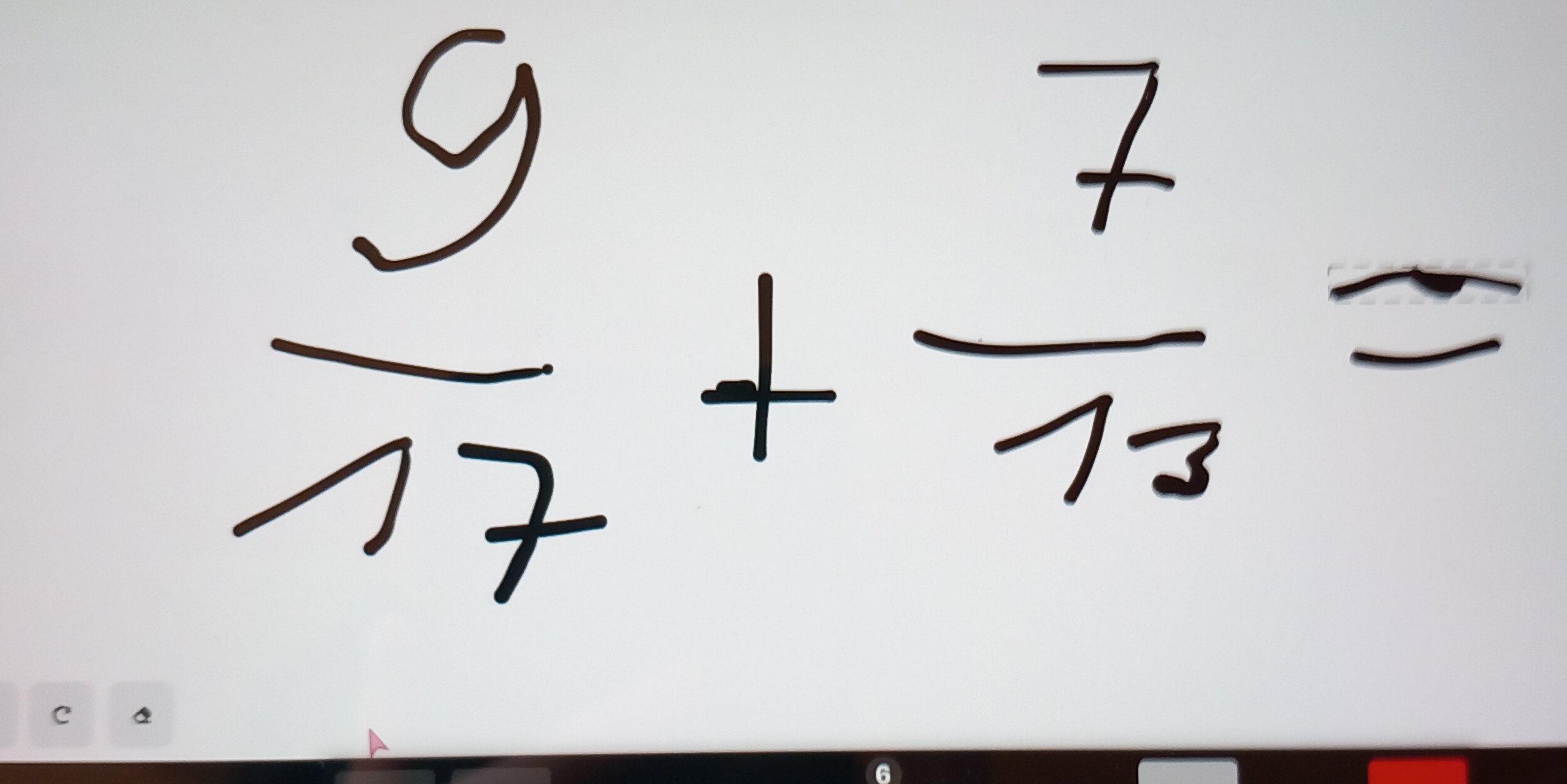
Understand the Problem
The question is asking to add two fractions, specifically 9/7 and 7/13. The task involves finding a common denominator and combining the fractions.
Answer
The sum of the fractions is $\frac{166}{91}$.
Answer for screen readers
The final answer is $\frac{166}{91}$.
Steps to Solve
- Find a common denominator
To add the fractions $\frac{9}{7}$ and $\frac{7}{13}$, we first find the least common denominator (LCD). The denominators are 7 and 13.
The LCD is found by multiplying the two denominators together if they have no common factors: $$ \text{LCD} = 7 \times 13 = 91 $$
- Convert the fractions
Next, we convert each fraction to have the common denominator of 91.
For $\frac{9}{7}$: $$ \frac{9}{7} = \frac{9 \times 13}{7 \times 13} = \frac{117}{91} $$
For $\frac{7}{13}$: $$ \frac{7}{13} = \frac{7 \times 7}{13 \times 7} = \frac{49}{91} $$
- Add the fractions
Now that both fractions have the same denominator, we can add them: $$ \frac{117}{91} + \frac{49}{91} = \frac{117 + 49}{91} = \frac{166}{91} $$
- Simplify if necessary
We check if $\frac{166}{91}$ can be simplified. Since 166 and 91 have no common factors, this fraction is already in its simplest form.
The final answer is $\frac{166}{91}$.
More Information
The result, $\frac{166}{91}$, is an improper fraction, meaning the numerator is greater than the denominator. It can also be expressed as a mixed number: $$ \frac{166}{91} = 1 \frac{75}{91} $$
Tips
- Forgetting to find the common denominator.
- Failing to convert both fractions properly before adding.
- Not simplifying the final fraction.
AI-generated content may contain errors. Please verify critical information