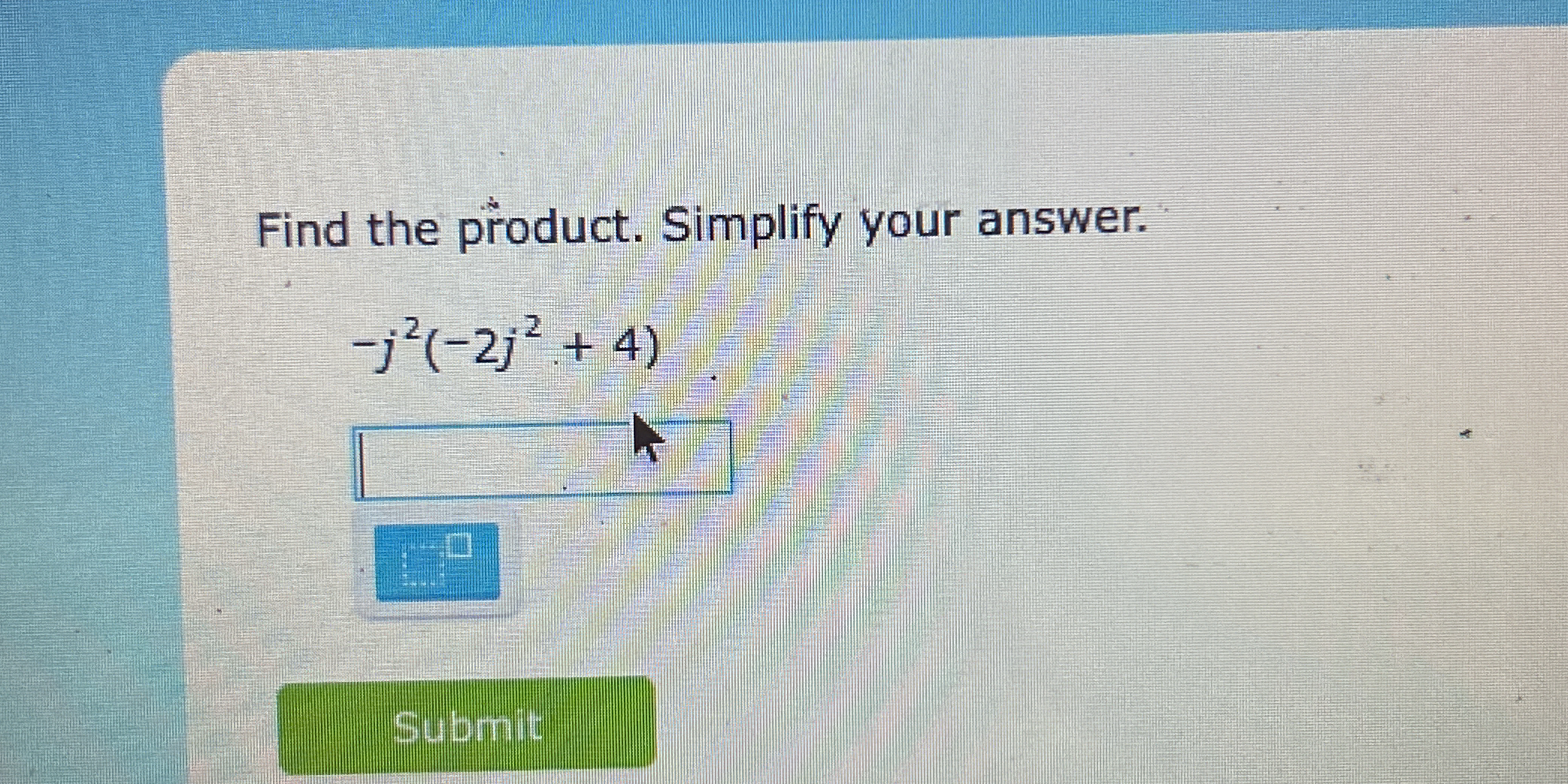
Find the product. Simplify your answer. -j²(-2j² + 4)
Understand the Problem
The question is asking to find the product of the expression -j²(-2j² + 4) and then simplify the answer. This involves algebraic manipulation, specifically focusing on the distribution and simplification of terms.
Answer
The simplified product is $2j^4 - 4j^2$.
Answer for screen readers
The simplified product of the expression is $2j^4 - 4j^2$.
Steps to Solve
- Distributing the expression
We start by distributing the term $-j^2$ across the expression $(-2j^2 + 4)$.
This gives us: $$ -j^2 \cdot -2j^2 + -j^2 \cdot 4 $$
- Calculating the first term
Now, let's calculate the first term: $$ -j^2 \cdot -2j^2 = 2j^{2+2} = 2j^4 $$
- Calculating the second term
Next, we calculate the second term: $$ -j^2 \cdot 4 = -4j^2 $$
- Combining the results
Now we can combine our two results: $$ 2j^4 - 4j^2 $$
The simplified product of the expression is $2j^4 - 4j^2$.
More Information
When multiplying expressions, it's important to remember that multiplying a negative and a negative gives a positive, which we did with the first term. The term $j^2$ raised to an exponent is also multiplied when you combine powers.
Tips
- Forgetting to distribute the negative sign correctly.
- Miscalculating the powers of $j$ when multiplying.
AI-generated content may contain errors. Please verify critical information