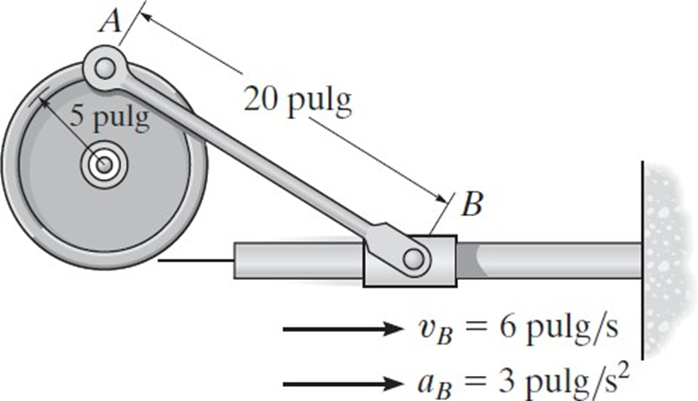
What are the velocities and accelerations in this pulley system involving points A and B?

Steps to Solve

1. Identify the system components

In this mechanical system, we have a pulley at point A and a connection to point B. The radius of the pulley is given as 5 pulg, and the distance from the center of the pulley to point B is 20 pulg.

2. Calculate the relationship between velocities

Using the formula for the relationship of velocities in a pulley system, we have:

$$ v_A = r_A \cdot \omega $$

where $r_A$ is the radius of the pulley (5 pulg), and the angular velocity $\omega$ can be derived from the linear velocity $v_B$ of point B:

$$ v_B = r_T \cdot \omega $$

Here $r_T$ is the length from the pivot of the pulley to point B (20 pulg).

From the given data, we can establish:

$$ v_A = \frac{r_A}{r_T} \cdot v_B $$

3. Substitute known values

Substituting $v_B = 6 , \text{pulg/s}$ into the equation we found:

$$ v_A = \frac{5}{20} \cdot 6 = \frac{1}{4} \cdot 6 = 1.5 , \text{pulg/s} $$

4. Calculate acceleration at point A

We also need to establish the relationship for accelerations, which follows the same principle:

$$ a_A = \frac{r_A}{r_T} \cdot a_B $$

Substitute $a_B = 3 , \text{pulg/s}^2$ into the equation:

$$ a_A = \frac{5}{20} \cdot 3 = \frac{1}{4} \cdot 3 = 0.75 , \text{pulg/s}^2 $$