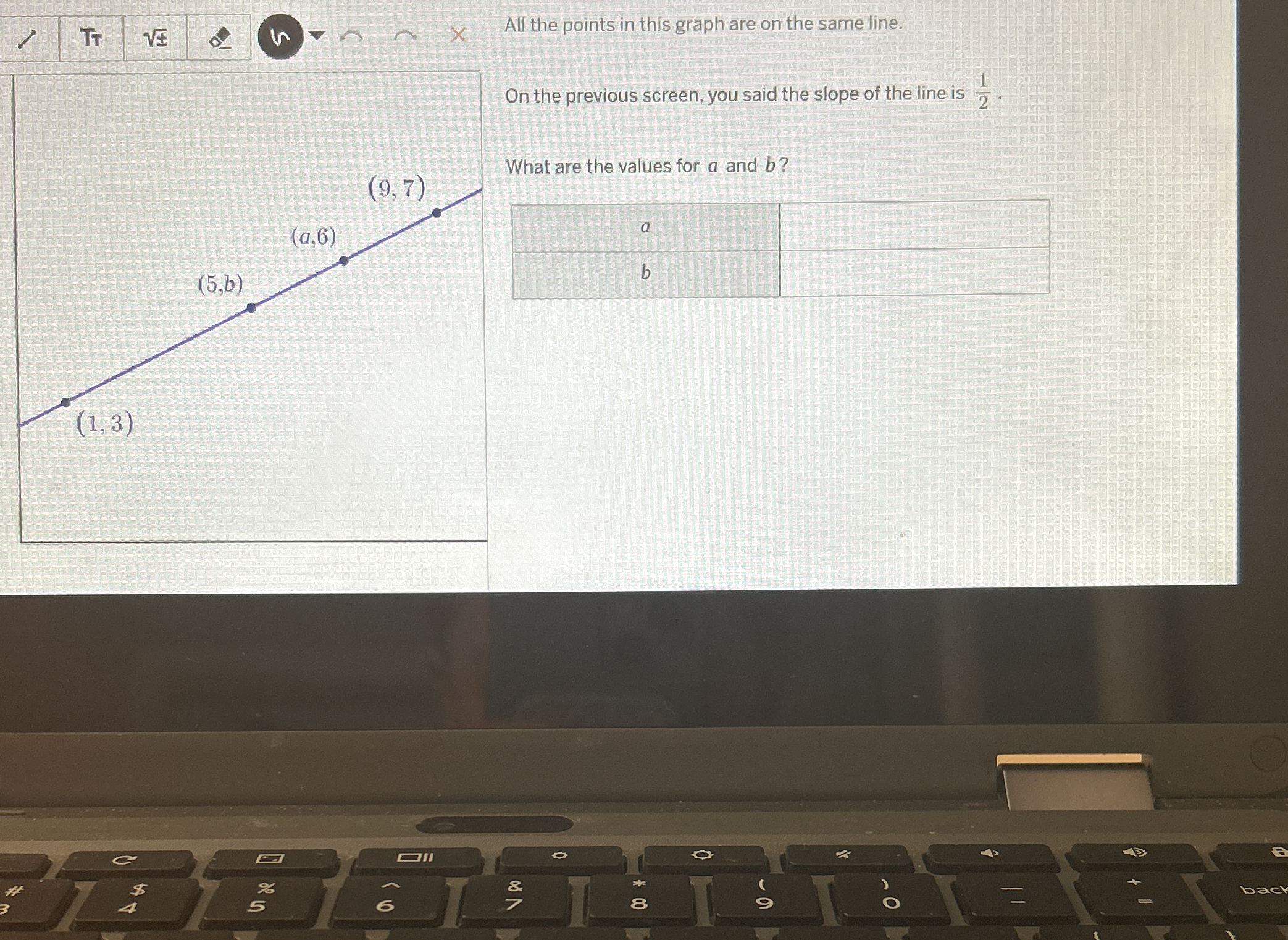
What are the values for a and b?

Steps to Solve

1. Identify the Known Points

   The known points provided in the problem are:

   • Point 1: $(1, 3)$
   • Point 2: $(9, 7)$
   • Point 3: $(5, b)$ (we need to find $b$)
   • Point 4: $(a, 6)$ (we need to find $a$)

2. Use the Given Slope

   The slope of a line between two points is calculated using the formula: $$ m = \frac{y_2 - y_1}{x_2 - x_1} $$ Here, the slope $m$ is given as $\frac{1}{2}$. We will use this to establish equations.

3. Calculate Point (1, 3) and (9, 7)

   Using points $(1, 3)$ and $(9, 7)$ to verify the slope:

   • Let $(x_1, y_1) = (1, 3)$ and $(x_2, y_2) = (9, 7)$.
   • Find the slope: $$ m = \frac{7 - 3}{9 - 1} = \frac{4}{8} = \frac{1}{2} $$ This confirms that the slope is correct.

4. Find the Value of b Using Point (5, b)

   Now using the point $(5, b)$ and one of the known points $(1, 3)$ to find $b$:

   • Let $(x_1, y_1) = (1, 3)$ and $(x_2, y_2) = (5, b)$.
   • The slope is again $\frac{1}{2}$: $$ \frac{b - 3}{5 - 1} = \frac{1}{2} $$
   • Simplifying gives: $$ \frac{b - 3}{4} = \frac{1}{2} $$
   • Cross-multiplying: $$ b - 3 = 2 \ b = 5 $$

5. Find Value of a Using Point (a, 6)

   Now using the point $(a, 6)$ and the known point $(9, 7)$ to find $a$:

   • Let $(x_1, y_1) = (9, 7)$ and $(x_2, y_2) = (a, 6)$.
   • Use the slope: $$ \frac{6 - 7}{a - 9} = \frac{1}{2} $$
   • Simplifying gives: $$ \frac{-1}{a - 9} = \frac{1}{2} $$
   • Cross-multiplying: $$ -2 = a - 9 $$
   • Rearranging: $$ a = 7 $$