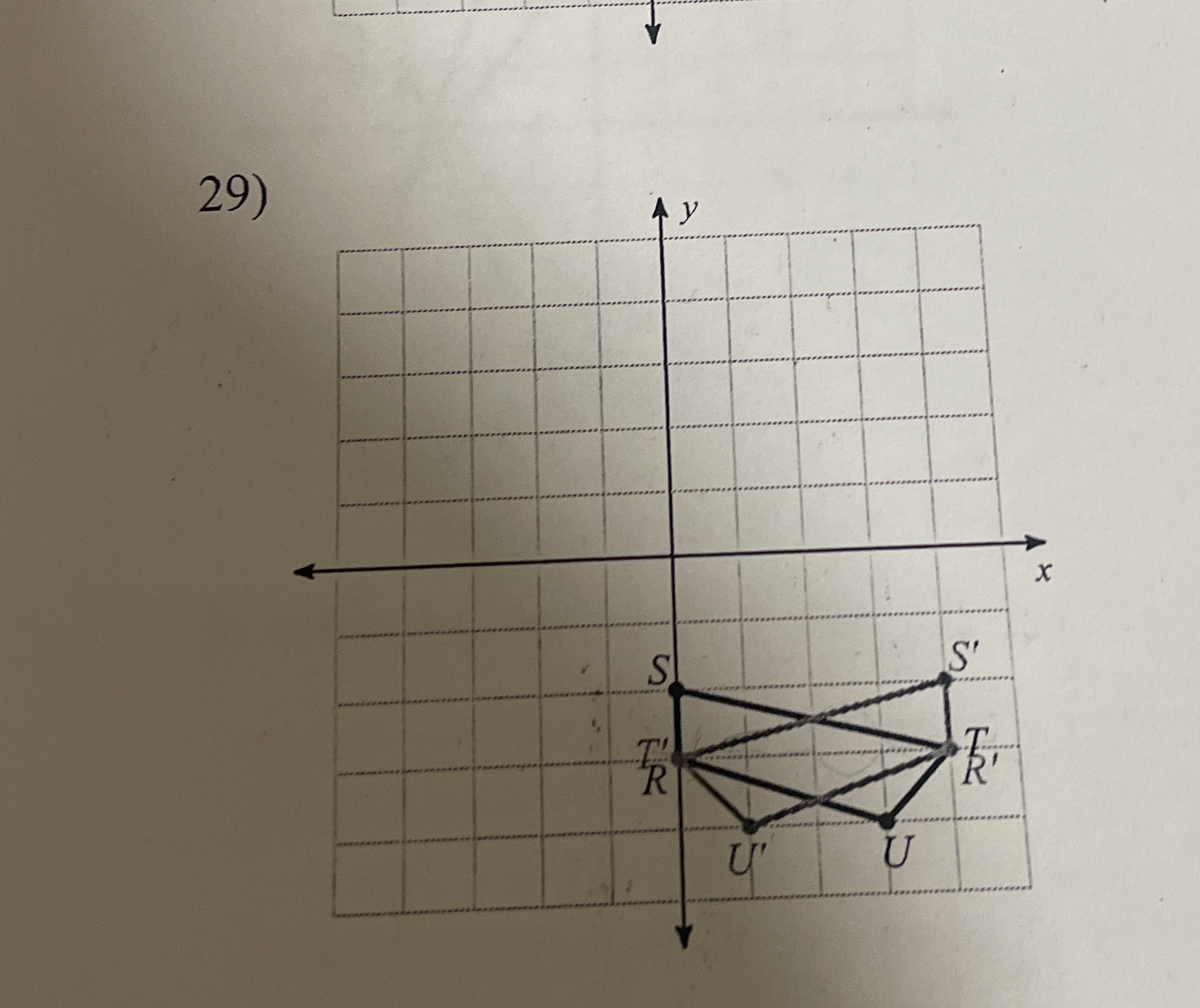
What are the transformations applied to the shapes represented in the given coordinate plane?
Understand the Problem
The question involves geometrical shapes and transformations represented on a coordinate plane, likely asking about properties such as symmetry or transformations like translation or reflection.
Answer
The transformation is a reflection across the x-axis.
Answer for screen readers
The transformation is a reflection across the x-axis.
Steps to Solve
-
Identify Points and Transformations Identify the original points and their transformed counterparts from the diagram. The points labeled are ( U, T, R ) and their corresponding transformed points ( U', T', R' ).
-
Determine the Type of Transformation Examine how the points have changed position. In this case, it appears that the shape formed by the points undergoes a reflection across the line ( y = 0 ) (the x-axis).
-
Check Coordinates Write down the coordinates of the original points and their images after transformation:
- ( U = (x_1, y_1) )
- ( T = (x_2, y_2) )
- ( R = (x_3, y_3) )
- The transformed points:
- ( U' = (x_1, -y_1) )
- ( T' = (x_2, -y_2) )
- ( R' = (x_3, -y_3) )
-
Confirm that the Properties Hold Validate that the distances between corresponding points remain equal and that the line formed by the original points is parallel to the line formed by the transformed points.
-
Conclude the Type of Transformation Conclude what type of transformation took place (in this case, reflection across the x-axis).
The transformation is a reflection across the x-axis.
More Information
A reflection across the x-axis means that every point ( (x, y) ) transforms to ( (x, -y) ). This transformation preserves distances and congruence of shapes.
Tips
- Mistaking reflection for translation, which would not maintain the original distances between points.
- Forgetting to check the coordinates of the original and transformed points to ensure accuracy.
AI-generated content may contain errors. Please verify critical information