What are the properties of the quadratic function represented in the graph?

Understand the Problem

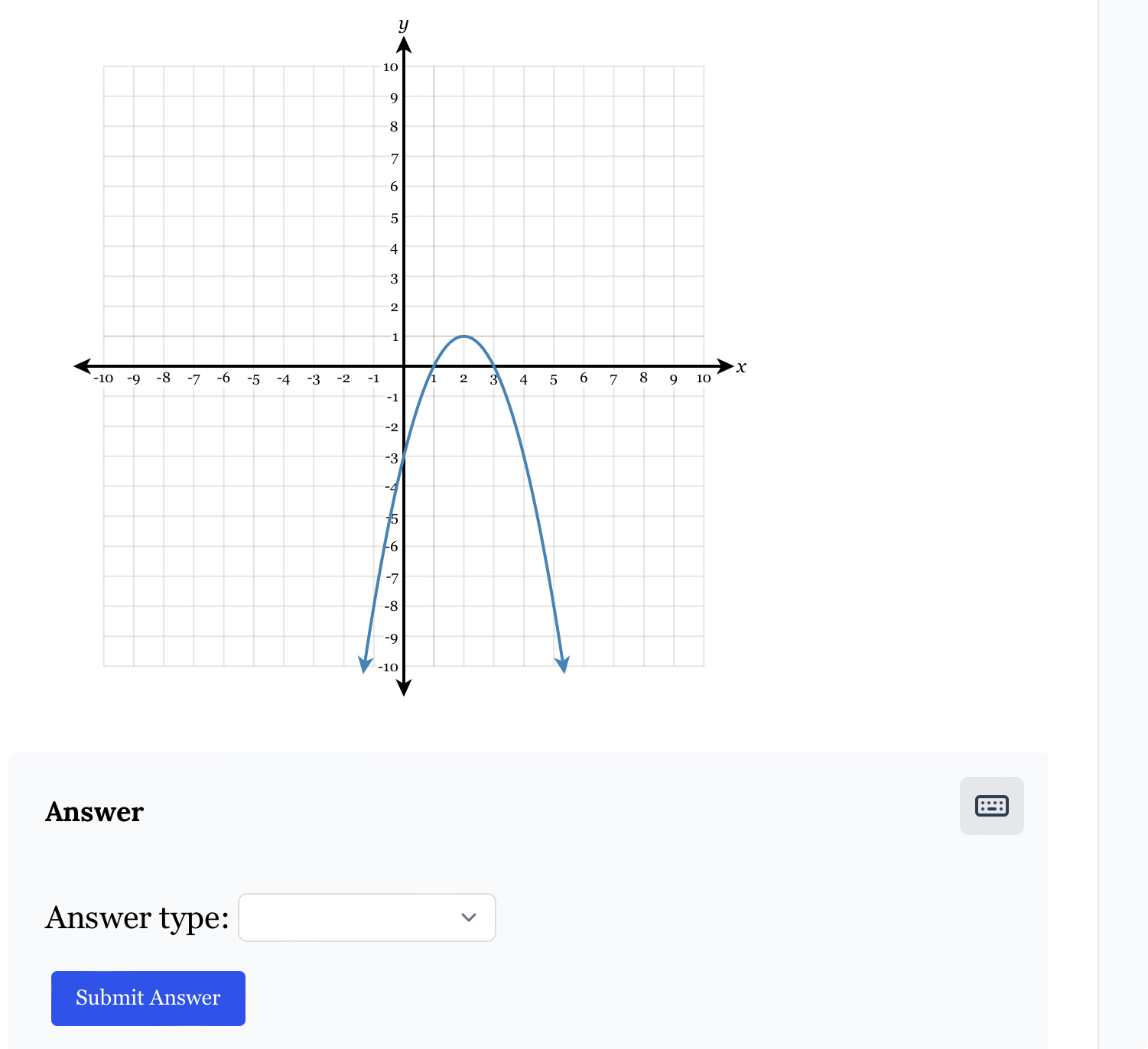
The graph shown appears to be a quadratic function, likely asking for properties such as the vertex, intercepts, or general characteristics of the function.

Answer

Vertex: $(3, -9)$; Y-intercept: $(0, -8)$; X-intercepts: $(1.5, 0)$ and $(4.5, 0)$.

Steps to Solve

Identify the Vertex The vertex of the quadratic function can be found at the lowest point on the graph. From observing the graph, the vertex appears to be at the point $(3, -9)$.
Determine the Y-intercept The Y-intercept is found where the graph crosses the Y-axis (where $x = 0$). From the graph, it crosses the Y-axis at $(0, -8)$.
Calculate the X-intercepts The X-intercepts occur where the graph crosses the X-axis (where $y = 0$). By interpolating the graph, the X-intercepts appear to be at approximately $x ≈ 1.5$ and $x ≈ 4.5$.
General Characteristics The quadratic function opens upwards (as the arms of the parabola are pointing up), indicating that the coefficient of $x^2$ is positive.
Summarizing Properties Summarize the key properties identified:

Vertex: $(3, -9)$
Y-intercept: $(0, -8)$
X-intercepts: $(1.5, 0)$ and $(4.5, 0)$
Opens upwards

The vertex is at $(3, -9)$, the Y-intercept is at $(0, -8)$, and the X-intercepts are approximately $(1.5, 0)$ and $(4.5, 0)$.

More Information

These properties are essential for understanding the behavior of a quadratic function, including its range, domain, and the location of its extrema. The vertex provides the minimum value of the function, and the intercepts demonstrate where it intersects the axes.

Tips

Misidentifying the vertex due to not recognizing the lowest or highest point in the graph.
Measuring the intercepts incorrectly by not checking where the graph touches the axes.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!