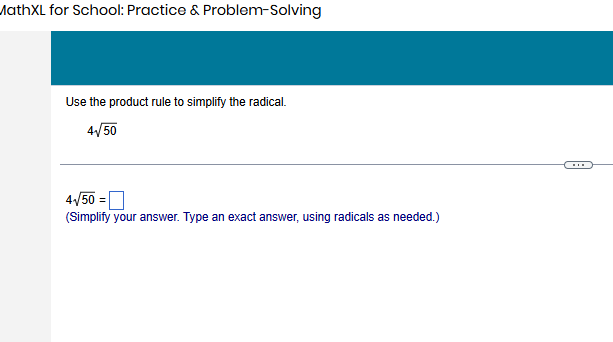
Simplify 4/50 using the product rule.

Steps to Solve

1. Express the fraction as a radical

We can write the fraction $\frac{4}{50}$ as a single radical expression: $$ \sqrt{\frac{4}{50}} $$

2. Simplify the fraction under the radical

Now, simplify the fraction inside the radical: $$ \sqrt{\frac{4}{50}} = \sqrt{\frac{4 \div 2}{50 \div 2}} = \sqrt{\frac{2}{25}} $$

3. Use the product rule for radicals

According to the product rule, we can break this radical into two: $$ \sqrt{\frac{2}{25}} = \frac{\sqrt{2}}{\sqrt{25}} $$

4. Simplify further

Since $\sqrt{25} = 5$, we can write: $$ \frac{\sqrt{2}}{\sqrt{25}} = \frac{\sqrt{2}}{5} $$