What are the properties of the adjoint of a matrix?
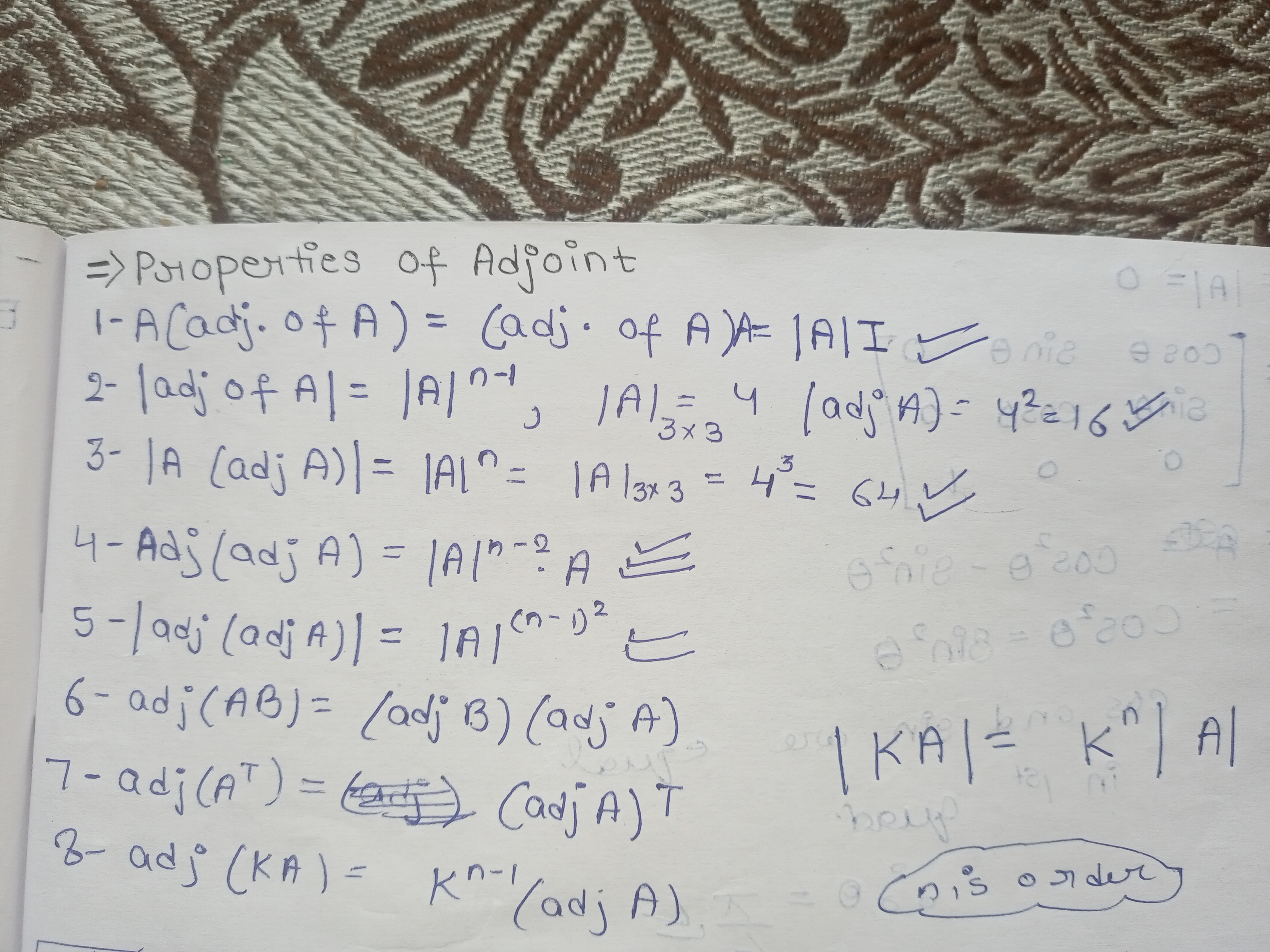
Understand the Problem
The question appears to be referring to the properties of adjoint matrices, listing several mathematical statements related to them. The focus seems to be on the application and implications of these properties in terms of determinants and matrix operations.
Answer
The properties of adjoint matrices connect determinants and matrix operations, highlighting formulas like \( A \cdot \text{adj}(A) = |A| I \).
Answer for screen readers
The properties of adjoints discussed demonstrate relationships involving determinants and matrix operations, ensuring a deeper understanding of how adjoint matrices function within the framework of linear algebra.
Steps to Solve
-
Understanding Adjoint Properties
The properties of the adjoint of a matrix relate the adjoint to determinants and the original matrix. The given properties are critical in linear algebra. -
Property 1: Multiplication with Adjoint
For any matrix ( A ), it holds that: $$ A \cdot (\text{adj}(A)) = (\text{adj}(A)) \cdot A = |A| I $$
This means multiplying the matrix ( A ) by its adjoint gives a scalar multiple of the identity matrix, where ( |A| ) is the determinant of ( A ). -
Property 2: Determinant of the Adjoint
The determinant of the adjoint of ( A ) can be expressed as: $$ |\text{adj}(A)| = |A|^{n-1} $$
where ( n ) is the order (size) of the square matrix ( A ). -
Property 3: Determinant in Product with Adjoint
The determinant of the product of ( A ) and its adjoint is: $$ |A \cdot (\text{adj}(A))| = |A|^n $$
This indicates that the determinant scales with the order of the matrix. -
Property 4: Adjoint of the Adjoint
The adjoint of the adjoint of ( A ) can be expressed as: $$ \text{adj}(\text{adj}(A)) = |A|^{n-2} A $$
This shows a relation between the adjoint of an adjoint and the original matrix. -
Property 5: Determinant of Adjoint of Adjoint
For the adjoint of adjoint, we have: $$ |\text{adj}(\text{adj}(A))| = |A|^{(n-1)^2} $$ -
Property 6: Adjoint of Product of Matrices
For matrices ( A ) and ( B ): $$ \text{adj}(AB) = \text{adj}(B) \cdot \text{adj}(A) $$
This property explains how to compute the adjoint of the product. -
Property 7: Adjoint of Transpose
The relationship between the adjoint and the transpose of a matrix is given by: $$ \text{adj}(A^T) = (\text{adj}(A))^T $$
This shows that the adjoint of the transpose is the transpose of the adjoint. -
Property 8: Adjoint with Scalar Multiplication
If a scalar ( k ) multiplies the matrix ( A ): $$ \text{adj}(kA) = k^{n-1} \cdot \text{adj}(A) $$
This property illustrates how scaling a matrix affects its adjoint.
The properties of adjoints discussed demonstrate relationships involving determinants and matrix operations, ensuring a deeper understanding of how adjoint matrices function within the framework of linear algebra.
More Information
Adjoint matrices play a vital role in calculating inverses, determinants, and linear transformations. The properties help simplify many calculations in linear algebra.
Tips
- Forgetting that the determinant ( |A| ) must be non-zero for an inverse to exist.
- Misapplying properties, especially when dealing with transposes and products of matrices.
- Confusing the scalar multiplication effect on the adjoint.
AI-generated content may contain errors. Please verify critical information