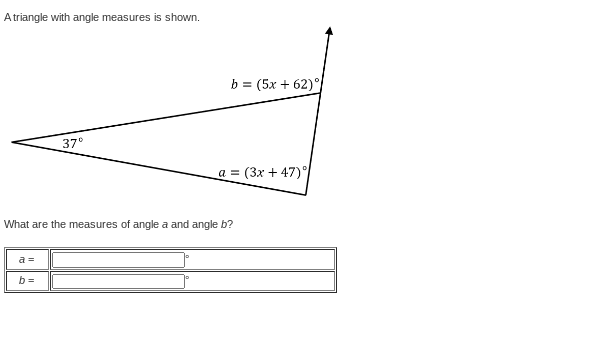
What are the measures of angle a and angle b?
Understand the Problem
The question is asking for the measures of angles a and b in a triangle. We need to set up an equation using the fact that the sum of the angles in a triangle equals 180 degrees, and then solve for the variable x to find the measures of both angles.
Answer
$a = 59.75°$ and $b = 83.25°$
Answer for screen readers
The measures of the angles are: $$ a = 59.75° \quad \text{and} \quad b = 83.25° $$
Steps to Solve
- Set up the equation using the triangle angle sum property
The sum of the angles in a triangle equals 180 degrees. We have three angles: $a$, $b$, and the given angle of 37°.
So, we can write the equation: $$ (5x + 62) + (3x + 47) + 37 = 180 $$
- Combine like terms
Combine the $x$ terms and the constant terms:
- The $x$ terms: $5x + 3x = 8x$
- The constant terms: $62 + 47 + 37 = 146$
Now the equation looks like: $$ 8x + 146 = 180 $$
- Isolate the variable $x$
Subtract 146 from both sides: $$ 8x = 180 - 146 $$ Calculating the right side gives: $$ 8x = 34 $$
- Solve for $x$
Now divide both sides by 8: $$ x = \frac{34}{8} = 4.25 $$
- Find angle a
Now substitute the value of $x$ back into the equation for angle $a$: $$ a = 3(4.25) + 47 = 12.75 + 47 = 59.75° $$
- Find angle b
Substituting $x$ back into the equation for angle $b$: $$ b = 5(4.25) + 62 = 21.25 + 62 = 83.25° $$
The measures of the angles are: $$ a = 59.75° \quad \text{and} \quad b = 83.25° $$
More Information
The angles in any triangle always sum up to 180 degrees. Here, angle $a$ is approximately 59.75 degrees and angle $b$ is approximately 83.25 degrees.
Tips
- Forgetting to sum all the angles, including the given angle of 37°.
- Miscalculating the sum of constants or $x$ terms while combining.
- Not properly following the order of operations when simplifying the equations.
AI-generated content may contain errors. Please verify critical information