What are the definitions of domain, codomain, and range in relation to the function f(x) = 2x + 1?
Understand the Problem
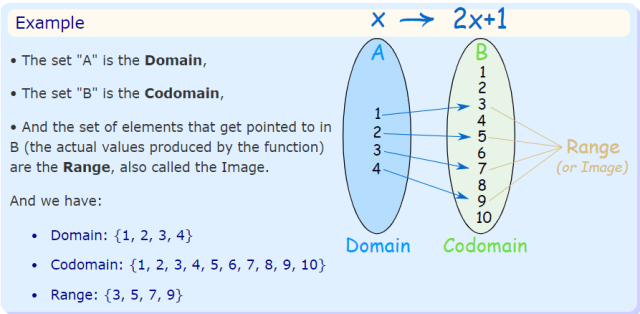
The question is explaining the concepts of domain, codomain, and range in the context of a function, specifically with the function f(x) = 2x + 1. It outlines the definitions of these terms and provides an example with specific sets for domain, codomain, and range.
Answer
Domain: all real numbers. Codomain: set defined by the context (often real numbers). Range: all real numbers.
The domain of f(x) = 2x + 1 is the set of all possible values of x, usually the set of all real numbers. The codomain is the set where the output values are allowed to fall, often predetermined by context or problem constraints. The range is the actual set of output values produced by the function, which for linear functions like this is also the set of all real numbers.
Answer for screen readers
The domain of f(x) = 2x + 1 is the set of all possible values of x, usually the set of all real numbers. The codomain is the set where the output values are allowed to fall, often predetermined by context or problem constraints. The range is the actual set of output values produced by the function, which for linear functions like this is also the set of all real numbers.
More Information
In functions, the domain determines the possible input values, the codomain specifies where outputs may fall, and the range is the subset of the codomain that the function actually maps to.
Tips
A common mistake is to confuse the codomain with the range. The codomain is a broader set that contains all possible outputs, while the range includes only the actual outputs for given domain inputs.
Sources
- Domain, Range and Codomain - Math is Fun - mathsisfun.com
- Domain Range and Codomain Of A Function - BYJU'S - byjus.com
AI-generated content may contain errors. Please verify critical information