What are the definitions and illustrations of concurrent lines, median of a triangle, and centroid?
Understand the Problem
The question is related to the definitions of geometric terms such as concurrent lines, median of a triangle, and centroid. It asks for clarity on these concepts and their illustrations in geometry.
Answer
Concurrent Lines: Intersect at one point. Median: Vertex to midpoint of opposite side. Centroid: Intersection of medians.
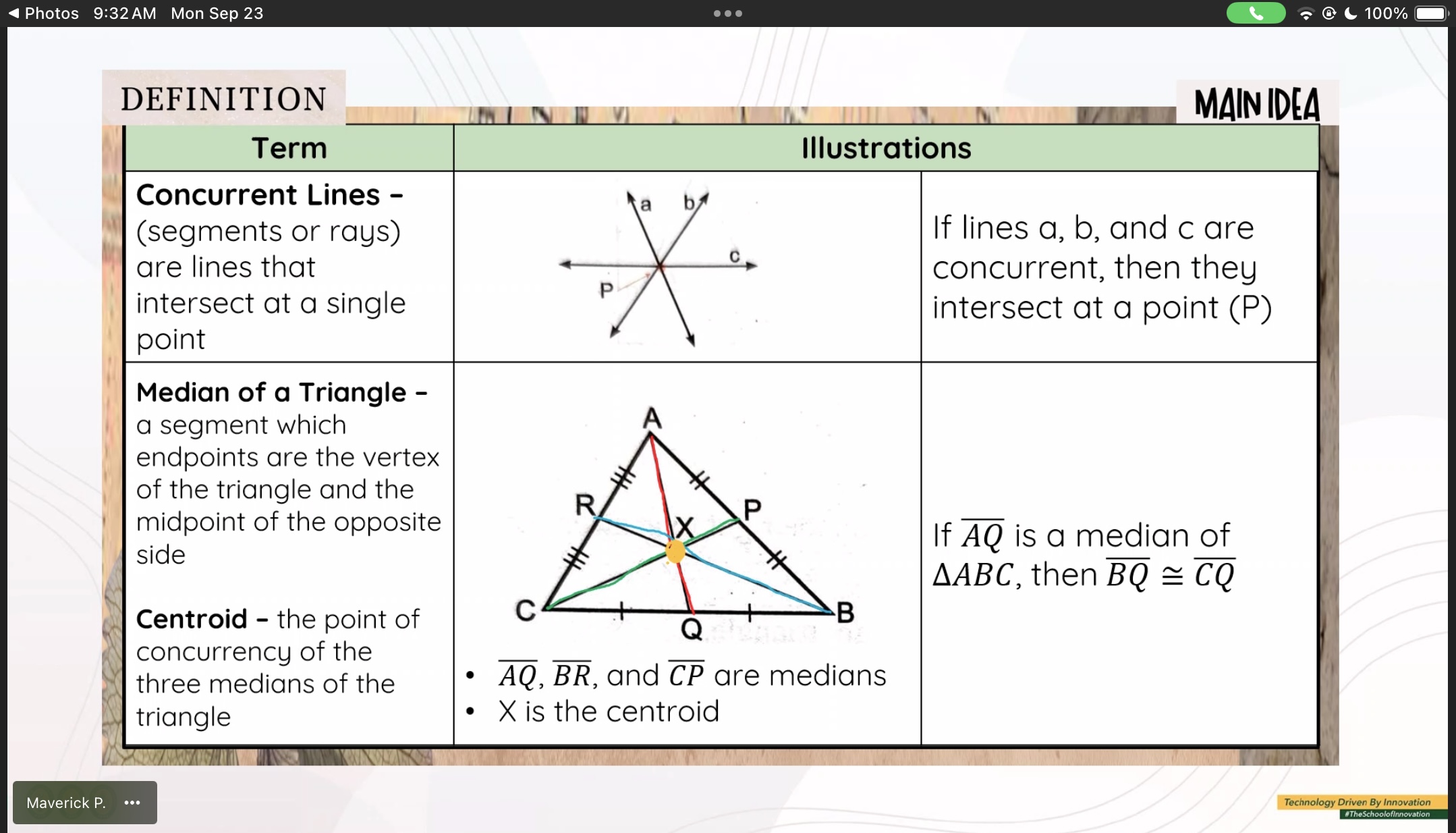
The definitions based on the image and search results are:
- Concurrent Lines: Lines that intersect at a single point. Illustrated as lines a, b, and c meeting at P.
- Median of a Triangle: A segment from a vertex to the midpoint of the opposite side. Illustrated with AQ, BR, and CP in triangle ABC.
- Centroid: The point of concurrency of the medians of a triangle. Illustrated as point X in triangle ABC.
Answer for screen readers
The definitions based on the image and search results are:
- Concurrent Lines: Lines that intersect at a single point. Illustrated as lines a, b, and c meeting at P.
- Median of a Triangle: A segment from a vertex to the midpoint of the opposite side. Illustrated with AQ, BR, and CP in triangle ABC.
- Centroid: The point of concurrency of the medians of a triangle. Illustrated as point X in triangle ABC.
More Information
The centroid, being the intersection of the medians, also acts as the triangle's center of mass. All medians intersect at a single point, illustrating a fundamental property of triangles.
Tips
Remember that concurrent lines must intersect at a single point, which can sometimes be confused with parallel lines that never intersect.
Sources
AI-generated content may contain errors. Please verify critical information