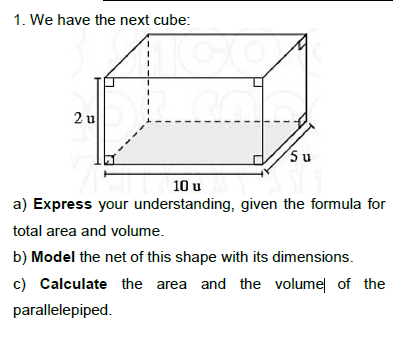
We have the next cube: a) Express your understanding, given the formula for total area and volume. b) Model the net of this shape with its dimensions. c) Calculate the area and the... We have the next cube: a) Express your understanding, given the formula for total area and volume. b) Model the net of this shape with its dimensions. c) Calculate the area and the volume of the parallelepiped.
Understand the Problem
The question is asking for three tasks related to a parallelepiped: first, to express the formulas for total area and volume; second, to model the net of the shape with dimensions; and third, to calculate the area and volume based on the given dimensions.
Answer
Total area: \( 160u^2 \), Volume: \( 100u^3 \)
Answer for screen readers
The total surface area of the parallelepiped is ( 160u^2 ) and the volume is ( 100u^3 ).
Steps to Solve
- Formulas for Total Area and Volume
The volume ( V ) of a parallelepiped is calculated using the formula:
[ V = l \cdot w \cdot h ]
where ( l ) is the length, ( w ) is the width, and ( h ) is the height.
The total surface area ( A ) is calculated using the formula:
[ A = 2(lw + lh + wh) ]
- Identify the Dimensions
From the given dimensions in the problem:
- Length ( l = 10u )
- Width ( w = 5u )
- Height ( h = 2u )
- Calculate Volume
Substituting the dimensions into the volume formula:
[ V = 10u \cdot 5u \cdot 2u ]
This simplifies to:
[ V = 100u^3 ]
- Calculate Total Area
Substituting the dimensions into the surface area formula:
[ A = 2(10u \cdot 5u + 10u \cdot 2u + 5u \cdot 2u) ]
Calculating each term:
[ = 2(50u^2 + 20u^2 + 10u^2) ] [ = 2(80u^2) = 160u^2 ]
- Visualizing the Net
To model the net of the parallelepiped, draw the shape consisting of six rectangles representing the faces:
- Two rectangles of size ( 10u \times 5u ) (front and back)
- Two rectangles of size ( 10u \times 2u ) (left and right)
- Two rectangles of size ( 5u \times 2u ) (top and bottom)
Label each rectangle with the corresponding dimensions.
The total surface area of the parallelepiped is ( 160u^2 ) and the volume is ( 100u^3 ).
More Information
The formulas used to calculate the total area and volume of a parallelepiped are fundamental in geometry, reflecting how three-dimensional shapes can be analyzed using their dimensions.
Tips
- Confusing volume and surface area formulas. Make sure to use the correct one for each calculation.
- Incorrectly identifying dimensions when substituting into the formulas. It's essential to clearly label and use the right dimensions.
AI-generated content may contain errors. Please verify critical information