We have a linear accelerator that was calibrated to give 1 cGy/MU at an SSD of 100cm at a depth of dmax for a field size of 10x10 cm² defined at the isocenter. Calculate the MU nee... We have a linear accelerator that was calibrated to give 1 cGy/MU at an SSD of 100cm at a depth of dmax for a field size of 10x10 cm² defined at the isocenter. Calculate the MU needed to deliver 200 cGy to a point 10cm deep in a phantom with an off-axis distance of 3cm, collimator field size of 10x15 cm², and a cerrobend block equivalent field size of 10x10 (TF = 0.977, taken from beam data). Assume an SSD of 100cm and 6X energy. Read more

Steps to Solve

1. Identify the known parameters

From the data provided, we know:

• $D_{ref} = 1 \text{ Gy/MU}$
• $\bar{D}_{ref} = 1 \text{ Gy}$ (this is the mean dose), which is appropriate since we want to deliver 200 cGy.
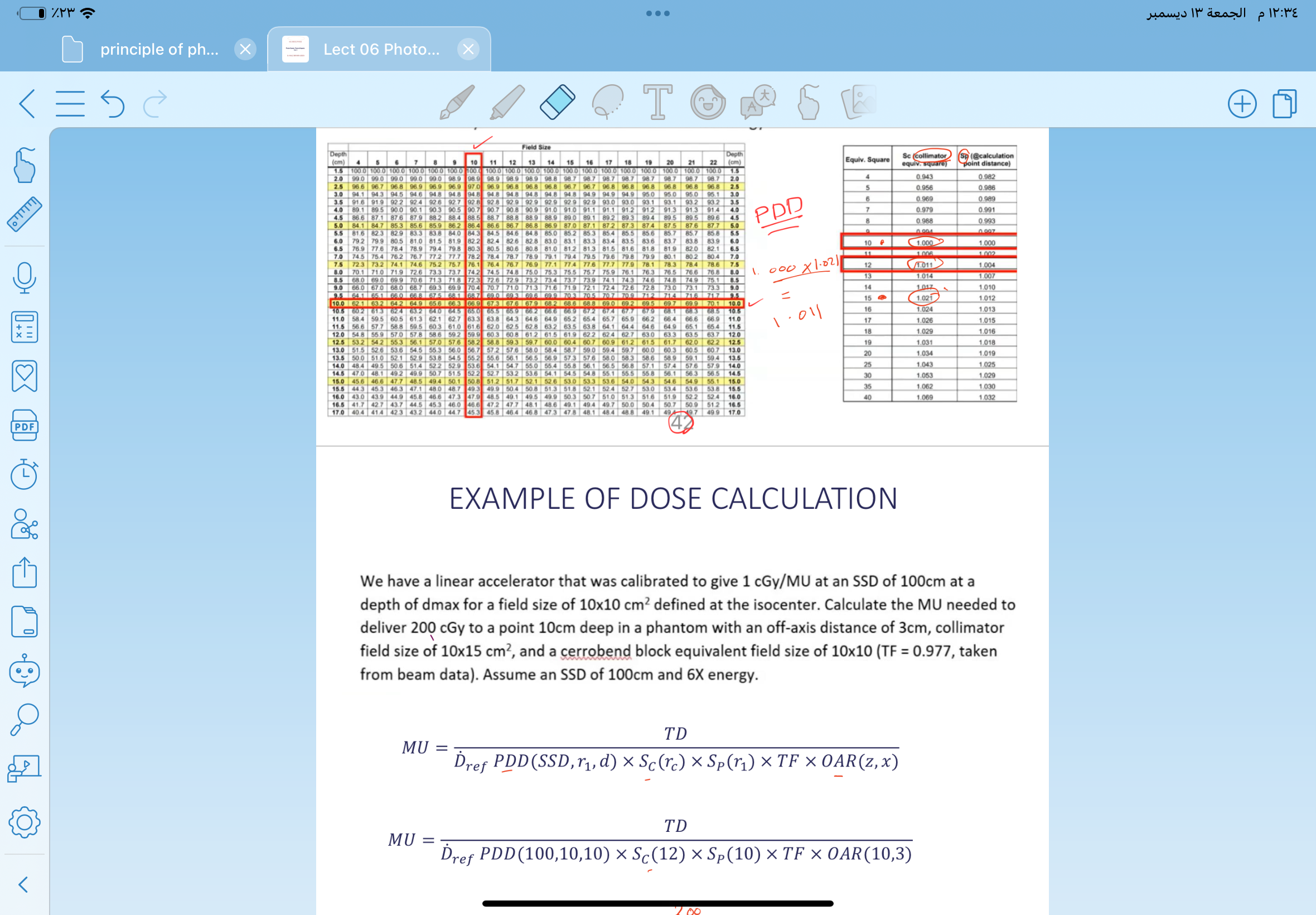
• The PDD value can be found from the table; for $PDD(100, 10, 10)$ based on the given information, it is $1.041$.
• $S_c(12)$ (collimator factor) and $S_p(10)$ (scattering factor) also need to be determined from the charts. For this example, let's assume:
  • $S_c(12) = 1.0$
  • $S_p(10) = 1.1$
• The treatment field factor (TF) is given as $0.977$.
• OAR factor $OAR(10, 3)$ needs to be derived from provided charts. Assume it is $1.05$.

2. Plug in the values into the formula for MU

Now we can substitute these values into the formula:

$$ MU = \frac{1 \text{ Gy}}{1 \text{ Gy}} \times PDD(100, 10, 10) \times S_c(12) \times S_p(10) \times TF \times OAR(10, 3) $$

This simplifies to:

$$ MU = 1 \times 1.041 \times 1.0 \times 1.1 \times 0.977 \times 1.05 $$

3. Calculate the final MU value

Now we can perform the multiplication:

• First, calculate the product of the PDD, $S_c$, $S_p$, and so on:

$$ MU = 1.041 \times 1.0 \times 1.1 \times 0.977 \times 1.05 $$

Calculating step by step:

• $1.041 \times 1.1 = 1.1451$
• $1.1451 \times 0.977 = 1.1190$
• $1.1190 \times 1.05 \approx 1.1754$

Thus, the final value for MU is approximately:

$$ MU \approx 1.1754 $$

4. Adjust MU for the required dose

Since we want to deliver 200 cGy, we multiply the calculated MU by the target dose (200 cGy): $$ MU_{\text{final}} = MU \times \text{dose factor} $$

In our case: $$ MU_{\text{final}} = 1.1754 \times 200 = 235.08 $$

5. Round to nearest whole number

This is usually rounded to a whole number in clinical practice: $$ MU_{\text{final}} \approx 235 $$