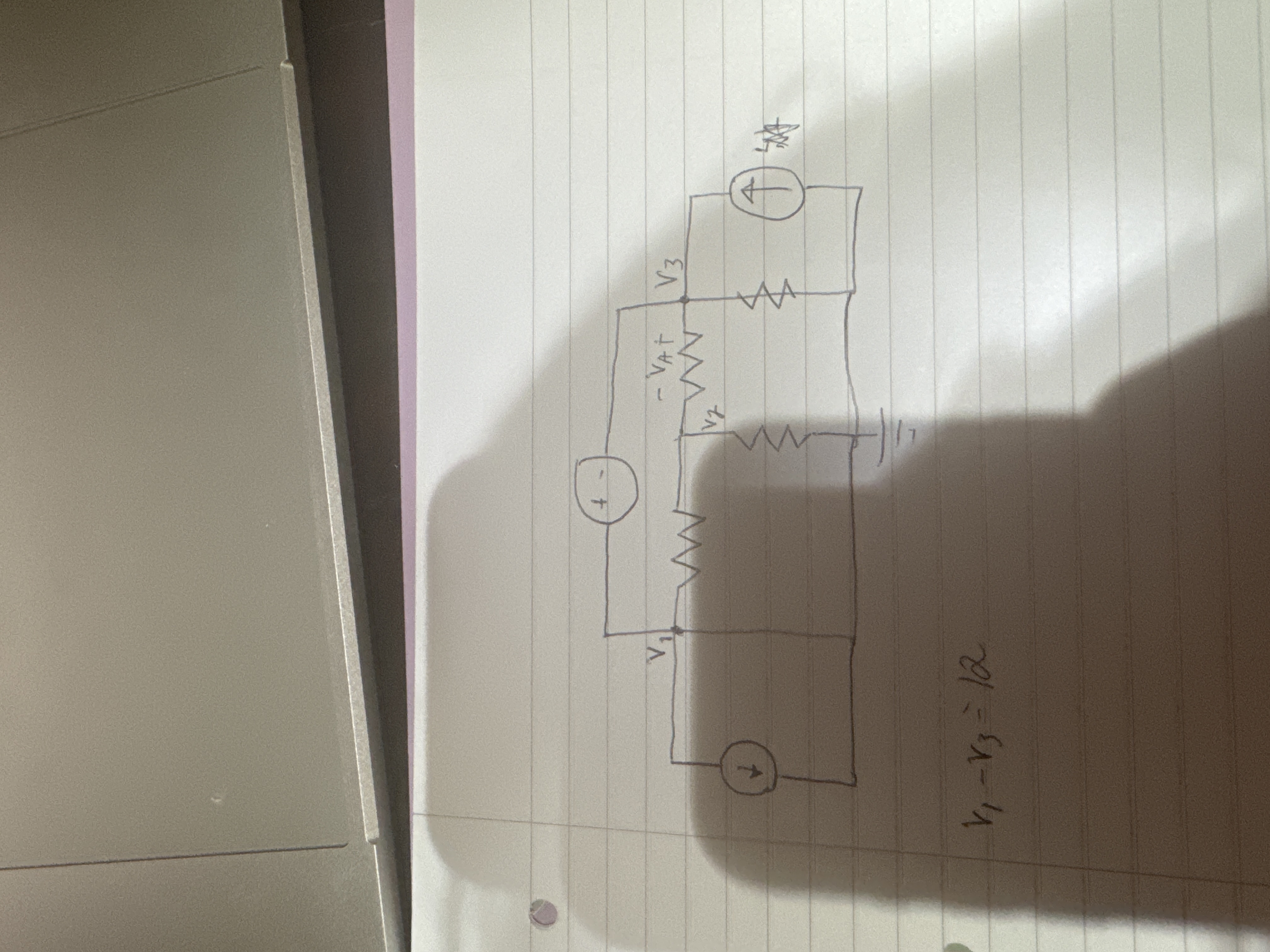
V1 - V3 = 12
Understand the Problem
The question involves analyzing an electrical circuit to solve for the voltages V1, V2, and V3, given an equation relating them (V1 - V3 = 12). This typically involves applying Kirchhoff's laws or other circuit analysis techniques.
Answer
$V_2 = 12$, $V_1 = 12 + V_3$.
Answer for screen readers
The final values for the voltages are:
- $V_2 = 12$
- $V_1 = V_3 + 12$ (depends on $V_3$)
- $V_3$ is a free variable; you can assign any value to $V_3$.
Steps to Solve
- Understanding the Circuit Setup
Identify the main components of the circuit. We have three voltages $V_1$, $V_2$, and $V_3$, and the equation given is $V_1 - V_3 = 12$.
- Applying Kirchhoff's Voltage Law
Kirchhoff's Voltage Law states that the sum of the potential differences (voltages) around any closed circuit is zero. For this circuit, we can write the following loop equation:
$$ V_1 - V_2 - V_3 = 0 $$
- Rearranging Equations
From the first equation, we can express $V_3$ as:
$$ V_3 = V_1 - 12 $$
Substituting this into the loop equation yields:
$$ V_1 - V_2 - (V_1 - 12) = 0 $$
- Simplifying the Equation
Simplifying the equation gives:
$$ -V_2 + 12 = 0 $$
Thus, we find:
$$ V_2 = 12 $$
- Substituting Back for Other Voltages
Using $V_2 = 12$ in the loop equation:
$$ V_1 - 12 - V_3 = 0 $$
This allows us to express $V_1$ in terms of $V_3$:
$$ V_1 = 12 + V_3 $$
- Final Relationships
We have now established relationships between the voltages:
- $V_2 = 12$
- $V_3 = V_1 - 12$
- $V_1 = 12 + V_3$
The final values for the voltages are:
- $V_2 = 12$
- $V_1 = V_3 + 12$ (depends on $V_3$)
- $V_3$ is a free variable; you can assign any value to $V_3$.
More Information
The voltage $V_2$ is fixed at 12 volts, while $V_1$ and $V_3$ can vary depending on the starting point of one voltage. The relationship derived from Kirchhoff’s laws allows us to explore different scenarios based on the circuit configuration.
Tips
- Confusing the signs when applying Kirchhoff's laws. Always pay attention to the direction of the current and the polarities of the terminals.
- Forgetting to rearrange equations correctly. Make sure to isolate the variables properly.
AI-generated content may contain errors. Please verify critical information