V = π ∫ from -1 to 1 (( (y - 1/2)² + (1 - y)² )) dy
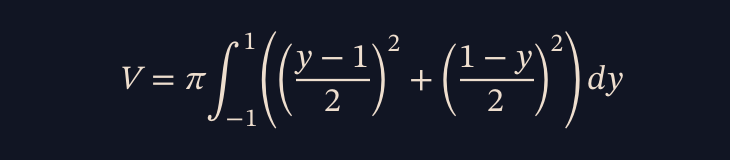
Understand the Problem
The question presents an integral that appears to calculate the volume of a solid of revolution. The approach will involve evaluating the integral using principles from calculus, particularly focusing on integration techniques.
Answer
The volume is \( V = \frac{4\pi}{3} \).
Answer for screen readers
The final volume is
$$ V = \frac{4\pi}{3} $$
Steps to Solve
- Set Up the Integral
The volume ( V ) is given by the integral
$$ V = \pi \int_{-1}^{1} \left( \left( \frac{y - 1}{2} \right)^{2} + \left( \frac{1 - y}{2} \right)^{2} \right) dy. $$
- Simplify Inside the Integral
Next, simplify the expression inside the integral.
First, calculate ( \left( \frac{y - 1}{2} \right)^{2} ) and ( \left( \frac{1 - y}{2} \right)^{2} ):
$$ \left( \frac{y - 1}{2} \right)^{2} = \frac{(y - 1)^{2}}{4} $$ $$ \left( \frac{1 - y}{2} \right)^{2} = \frac{(1 - y)^{2}}{4} $$
The combined expression becomes: $$ \frac{(y - 1)^{2}}{4} + \frac{(1 - y)^{2}}{4} = \frac{1}{4}((y - 1)^{2} + (1 - y)^{2}) $$
- Calculate the Squared Terms
Next, expand ( (y - 1)^{2} + (1 - y)^{2} ):
$$ (y - 1)^{2} = y^{2} - 2y + 1 $$ $$ (1 - y)^{2} = y^{2} - 2y + 1 $$
Thus, $$ (y - 1)^{2} + (1 - y)^{2} = 2y^{2} - 4y + 2 $$
- Integrate the Simplified Expression
Now replace the original integral with the simplified version:
$$ V = \pi \int_{-1}^{1} \frac{1}{4} (2y^{2} - 4y + 2) dy $$
This simplifies to:
$$ V = \frac{\pi}{4} \int_{-1}^{1} (2y^{2} - 4y + 2) dy $$
- Break Down the Integration
Now, split the integral:
$$ V = \frac{\pi}{4} \left( \int_{-1}^{1} 2y^{2} dy - 4 \int_{-1}^{1} y dy + 2 \int_{-1}^{1} 1 dy \right) $$
- Evaluate Each Integral
- For ( \int_{-1}^{1} 1 , dy ):
$$ \int_{-1}^{1} 1 , dy = 2 $$
- For ( \int_{-1}^{1} y , dy ):
$$ \int_{-1}^{1} y , dy = 0 $$
- For ( \int_{-1}^{1} 2y^{2} , dy ):
$$ \int_{-1}^{1} 2y^{2} , dy = 2 \cdot \left( \frac{y^{3}}{3} \Big|_{-1}^{1} \right) = 2 \cdot \left( \frac{1}{3} - \left(-\frac{1}{3}\right) \right) = \frac{4}{3} $$
Putting all of this back into the expression for ( V ):
$$ V = \frac{\pi}{4} \left( \frac{4}{3} - 0 + 2 \cdot 2 \right) = \frac{\pi}{4} \left( \frac{4}{3} + 4 \right) = \frac{\pi}{4} \left( \frac{4 + 12}{3} \right) = \frac{\pi}{4} \cdot \frac{16}{3} = \frac{4\pi}{3} $$
The final volume is
$$ V = \frac{4\pi}{3} $$
More Information
This volume represents the solid formed by revolving the specified region around an axis. The calculations involve both standard integral evaluation and symmetries in the given functions.
Tips
- Neglecting the symmetry of the function and thus not realizing that some terms will cancel out.
- Incorrectly simplifying the terms before integration.
AI-generated content may contain errors. Please verify critical information