U(x,t) = A Cos(nπ/a x), A = ?, <x> = ?, <x^2> = 2, W = ?
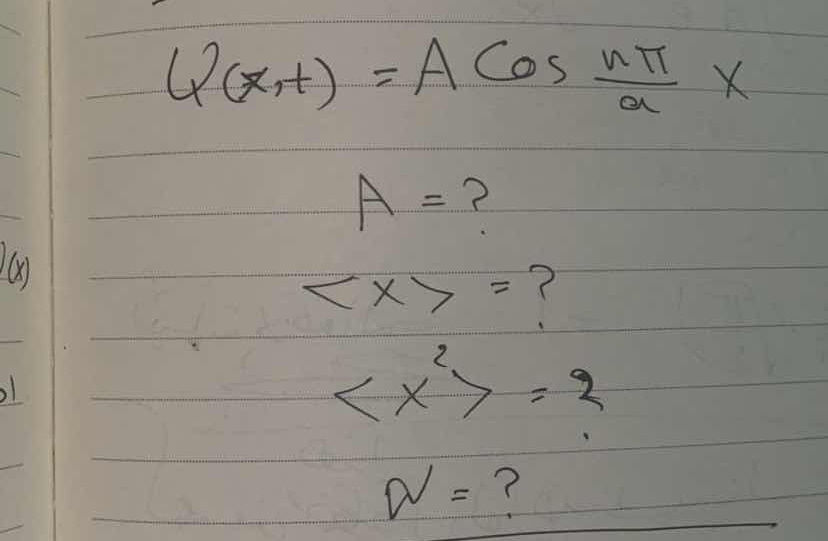
Understand the Problem
The question appears to be a physics or mathematics problem involving a wave function. It asks for the value of 'A' in the equation, as well as the expected values of
Answer
$A = \sqrt{\frac{2}{a}}$; $\langle x \rangle = \frac{a}{2}$; $\langle x^2 \rangle = 2$; $W = -\frac{\hbar^2 \pi^2 n^2}{2m a^2}$.
Answer for screen readers
- The value of $A$ is $A = \sqrt{\frac{2}{a}}$.
Steps to Solve
-
Identify the Function The given wave function is $U(x,t) = A \cos\left(\frac{n\pi}{a} x\right)$.
-
Normalize the Wave Function To find the value of $A$, we normalize the wave function. The normalization condition is: $$ \int_0^a |U(x,t)|^2 dx = 1 $$ Substituting the wave function, we have: $$ \int_0^a |A \cos\left(\frac{n\pi}{a} x\right)|^2 dx = 1 $$
-
Calculate the Integral The integral becomes: $$ A^2 \int_0^a \cos^2\left(\frac{n\pi}{a} x\right) dx $$ Using the identity $\cos^2(\theta) = \frac{1 + \cos(2\theta)}{2}$: $$ \int_0^a \cos^2\left(\frac{n\pi}{a} x\right) dx = \frac{a}{2} $$ Thus the equation simplifies to: $$ A^2 \cdot \frac{a}{2} = 1 $$
-
Solve for A From the normalization we have: $$ A^2 = \frac{2}{a} \implies A = \sqrt{\frac{2}{a}} $$
-
Calculate the Expected Values The expected value $\langle x \rangle$ for a particle in a box (0 to $a$) is: $$ \langle x \rangle = \frac{a}{2} $$ Since we are given $\langle x^2 \rangle = 2$, we'll use this value directly.
-
Calculate the Work W The work done, generally related to the energy of the wave function, can be calculated as: $$ W = \langle H \rangle = -\frac{\hbar^2 \pi^2 n^2}{2m a^2} $$ However, we need more information (like $n$, mass $m$, and $\hbar$) to compute a numeric value.
- The value of $A$ is $A = \sqrt{\frac{2}{a}}$.
More Information
- The wave function's normalization is crucial for quantum mechanics, ensuring probabilities are correctly calculated. The constant $A$ ensures the total probability of finding a particle is 1.
Tips
- One common mistake is forgetting to normalize the wave function correctly or miscalculating the integral. Ensure the integration bounds and functions are accurate.
AI-generated content may contain errors. Please verify critical information