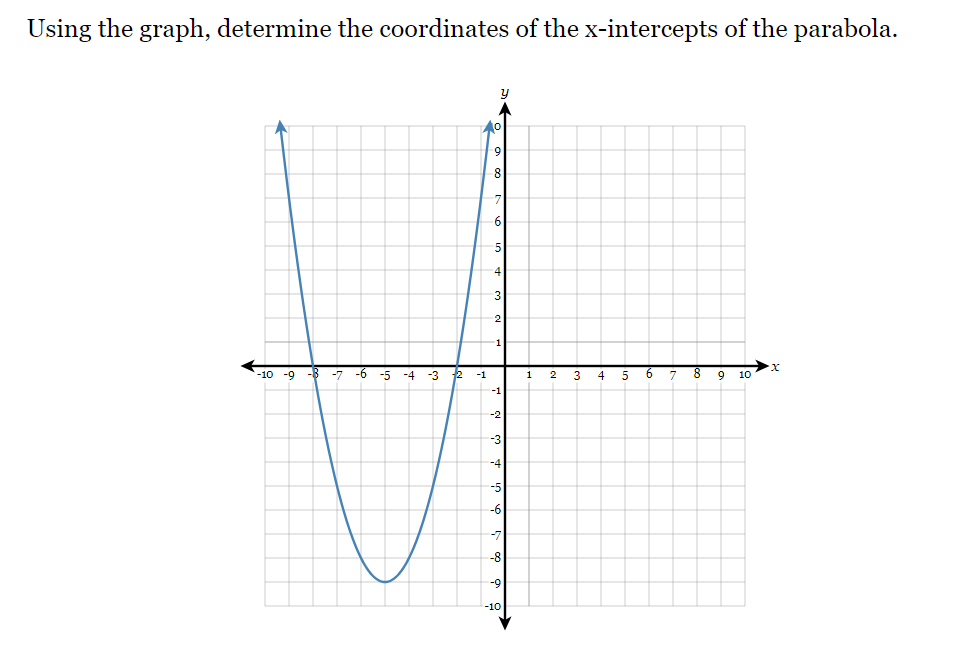
Using the graph, determine the coordinates of the x-intercepts of the parabola.
Understand the Problem
The question is asking to find the coordinates of the x-intercepts of a parabola based on the provided graph. The x-intercepts are the points where the graph crosses the x-axis, meaning the y-coordinate at those points is zero.
Answer
The coordinates of the x-intercepts are $(-6, 0)$ and $(-4, 0)$.
Answer for screen readers
The coordinates of the x-intercepts of the parabola are $(-6, 0)$ and $(-4, 0)$.
Steps to Solve
-
Identify the x-intercepts To find the x-intercepts of the parabola, look for the points where the graph crosses the x-axis. This occurs when the y-coordinate is equal to zero.
-
Read the coordinates from the graph Observe the graph and identify the x-values at which the curve intersects the x-axis. From the graph, the x-intercepts appear to be at approximately $x = -6$ and $x = -4$.
-
Write the coordinates The coordinates of the x-intercepts can now be stated as points on the Cartesian plane, which are written in the form $(x, y)$. For our x-intercepts, the coordinates will be:
- $(-6, 0)$
- $(-4, 0)$
The coordinates of the x-intercepts of the parabola are $(-6, 0)$ and $(-4, 0)$.
More Information
The x-intercepts are important in understanding the behavior of the parabola, particularly when solving quadratic equations, as they indicate the roots of the equation.
Tips
- Misreading the graph: It’s easy to confuse where the curve crosses the x-axis, especially if the graph is not perfectly aligned. Always double-check the points.
- Ignoring other intersections: Sometimes a graph may cross the x-axis multiple times. Ensure that you capture all x-intercepts.
AI-generated content may contain errors. Please verify critical information