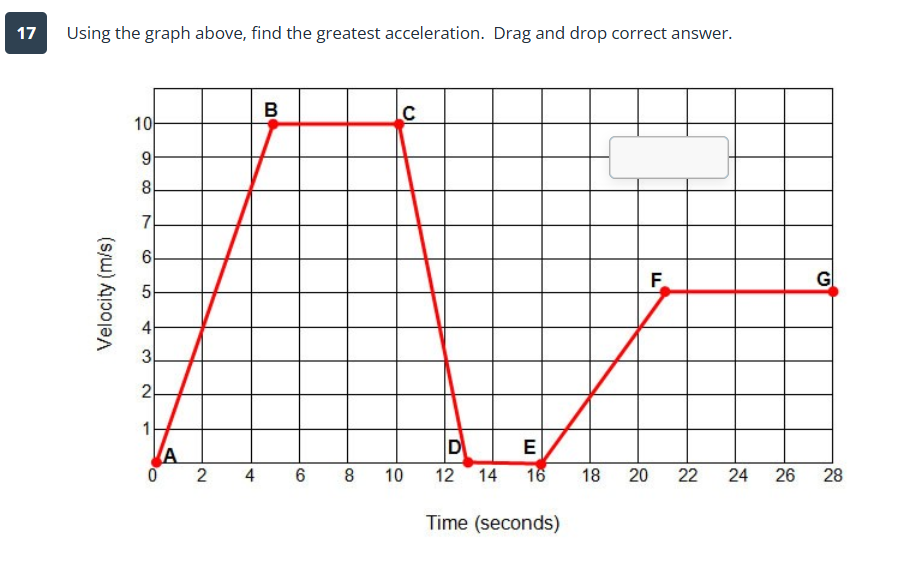
Using the graph above, find the greatest acceleration. Drag and drop the correct answer.
Understand the Problem
The question is asking to analyze the velocity graph provided to determine the point of greatest acceleration, which corresponds to the steepest slope on the graph.
Answer
The greatest acceleration occurs between points C and D.
Answer for screen readers
The point of greatest acceleration occurs between points C and D, where the slope is steepest.
Steps to Solve
-
Identify the Slope of the Graph Examine the velocity graph to find segments where the slope (which represents acceleration) is steepest. Acceleration occurs when the velocity is changing over time, which is represented by the rise over run.
-
Determine the Segments of Interest Note the segments where the graph slopes upward (accelerating) and downward (decelerating). The vertical lines represent instances of constant velocity (no acceleration).
-
Calculate the Slope For each segment where the graph is sloped, calculate the slope using the formula: $$ \text{slope} = \frac{\text{change in velocity}}{\text{change in time}} $$
-
Compare Slope Values Evaluate the slopes of the segments identified earlier and compare them to determine which one represents the greatest acceleration.
-
Identify the Point of Greatest Acceleration Select the point at which the greatest value of the slope (highest acceleration) occurs.
The point of greatest acceleration occurs between points C and D, where the slope is steepest.
More Information
The steepness of the slope indicates the rate of change of velocity. Greater slopes correspond to higher accelerations.
Tips
Null
AI-generated content may contain errors. Please verify critical information